福島周辺における空間線量率の測定と評価
-環境ガンマ線の特徴と被ばく線量との関係-
※本解説はRadioisotope,63,12,p.585-602(斎藤・遠藤、2014)による。
1. はじめに
福島事故やチョルノービリ(チェルノブイリ)事故のような大きな事故により放出された放射性物質は、長期にわたり環境中に存在し住民に被ばくを与えるため1)、被ばく線量を適切に評価することが重要である。福島事故においては、食品中に含まれる放射性物質の確認が厳重に行われており、今後、大きな内部被ばくが起きる可能性は小さい。本稿においては、福島事故に起因する環境線源からのγ線による外部被ばくについて、実測される空間線量率や放射性核種の沈着量などから被ばく線量率を評価する方法について紹介する。
環境γ線による被ばくを評価する際には、環境特有の条件を考慮することが必要とされる。環境特有の条件の一つはγ線源となる放射性物質が環境中で特徴的な分布をすることであり、もう一つは被ばくの対象となる人間が広い年齢層にわたることである。
環境中に分布した放射性物質から放出されたγ線は、人体に入射する時点では線源条件により決まる独特の入射方向分布及びエネルギー分布を持つこととなる。この性質を十分に考慮して被ばく線量を評価することが必要である。例えば、人体へのγ線の入射方向分布を、回転対称入射(ROT)や等方入射(ISO)と近似して線量評価を行うことも可能ではあるが2)、実際の入射分布は厳密にはこれらとは異なる。ROTは人体軸を中心に360°全方向から平行ビームが対称に入射する場合を、ISOは全ての方向から平行ビームが均等に入射する場合をそれぞれ示している。
環境中には乳児から成人まであらゆる年齢の人間が存在して被ばくの対象となることも、施設内での被ばくとは異なる点である。体が小さくなるほど、体自身によるγ線の遮蔽効果も小さくなり、被ばく線量が大きくなる傾向にある。
環境γ線特有の入射方向分布やエネルギー分布を考慮して、また広い年齢層を対象とし被ばく線量を評価するための研究は以前から行われてきたが3),4)、最近、国際放射線防護委員会(ICRP)の新しい2007年勧告5)に対応する被ばく線量を評価する研究成果も発表された6)大本稿では、これら最近の研究を中心に、過去の関連した研究も含めて要点を紹介する。
2. 典型的な環境線源からのγ線場の特徴
2.1 環境中における放射性物質の分布
原子力施設から大気中に放出された放射性物質は、大気の動きに従って移流・拡散していく。放出源から近い地域では、図1に示すように、大気中の放射性物質はプルーム軸に垂直方向に濃度が正規分布をすると仮定したガウスプルームモデル8)で近似されることが多い。ここでプルームとは、気体状の物質が煙突から放出された煙のように大気とともに流れる状態を指す。一方、放出源からある程度離れた地域においては、放射性物質は空中に一様に近い形で分布するようになる。ガウスプルームモデルが放出点からどの程度の距離まで成り立つかは、大気の安定度によって様々である。
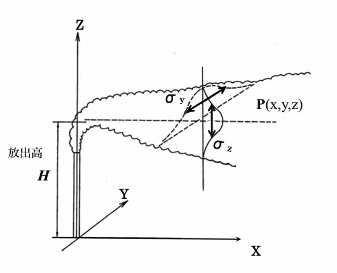
図1 ガウスプルームの概念図
大気中の放射性物質濃度はプルーム軸に垂直方向に正規分布をすると仮定している。
プルームの吹上げがあるため、モデルにおける放出高は実際の煙突の高さよりも高く想定される。
空中の放射性物質は降雨や降雪を通して地上に落ちる湿性沈着、及び降雨等を介さない乾性沈着により地表面や地上の物体に沈着して新たな線源となる。これら、地上の様々な物体に沈着した放射性物質は経過時間とともに、沈着した媒体の性質により異なる移行の様子を示す。アスファルトやコンクリート等の人工建造物に沈着した放射性物質のかなりの部分は、ウェザリング効果(風雨などの自然要因による移動)で比較的早く除去される性質があることがチョルノービリ(チェルノブイリ)事故後の研究で明らかになっている9)。一方、森林に沈着した放射性物質の動きは非常に遅いことが、チョルノービリ事故の経験においても1)また今回の福島事故後の調査でも10)明らかにされている。
土壌に沈着した放射性物質は、時間とともに徐々に地中に浸透していき、深さ方向の指数関数で近似される濃度分布をする11)。実際に福島事故の後に経時的に行われてきた大規模調査の結果でも、多くの測定点において地中に指数関数分布する放射性セシウムが観察されている10)。指数関数分布では、深さ ζ (g/cm2)における土壌中の放射性核種濃度A( ζ )(Bq/kg)は式(1)で表される11)。
深さ ζ の単位はcmではなくてg/cm2がよく使用される。これは地中の線源濃度と地上の空間線量率がg/cm2で表した深さにより関係づけられる性質があるためである。線源と地上までの間にどの程度の質量の上が存在するかが、γ線の遮蔽の程度を決定する重要な要因であることを表している。例えば、密度2g/m3の土壌中の深さ1cmにある線源と、密度1g/cm2の土壌中の深さ2cmにある線源は、いずれも ζ =2g/cm2であり、土による遮蔽効果は同程度であることになる。式(1)は以下の通りである。
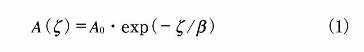
ここで、A0(Bq/kg)は地表面における放射性核種濃度、β(g/cm2)は放射性物質の地中への浸透の程度の指標となる緩衝深度である。緩衝深度は、放射性核種濃度が地表面の1/e(約1/2.72;eはネピア数)になる深さで定義される。福島事故後の調査において、平均的なβの値は経時的に徐々に増加してきている。すなわち地中の放射性セシウムが深い方向へ少しずつ浸透しつつある10) 一方、238U系列核種、232Th系列核種、40Kの天然放射性核種は一様分布に近い形で地中に存在する。同じ地中に存在する線源でも、地表面近くに大部分が存在する沈着線源とは深さ方向に異なる濃度分布を持ち、これに起因して地上のγ線場も後で見るようにそれぞれ特徴的な様相を示す。
2.2 典型的な環境線源によるγ線場の特徴
環境中に分布した線源からやってくるγ線は、移動の途中で空気や土による散乱や吸収を受けるため、線源から放出されるγ線が単色エネルギーであっても地上1mにおいてはエネルギー分布を持つし、入射方向分布も各線源分布に特有な分布を示す。また、福島周辺においては、地表からの高さにより空間線量率が顕著に減少する傾向があることが観察されているが、これは地表面に沈着した線源によるγ線場の特徴である。
2.2.1 入射方向分布
空中の一様分布体積線源、地表面付近(0.5g/cm2の深さ)の面線源(沈着面線源)、地中の一様分布体積線源からのγ線による地上1mの空気カーマ(Gy:空気吸収線量と実質的に同じ)の入射方向分布を図2に示す12)。これらの図では、γ線の進行方向と地面に垂直なベクトルがつくる角度の余弦(cosθ)を横軸にとり、縦軸には全空気カーマを1に規格化した角度ごと(単位立体角あたり)の空気カーマの比率を示している。cosθ=-1はγ線が真上から真下に向かって入射する場合、1はその逆、また0は真横から水平にγ線が入射する場合に相当する。線源分布によりそれぞれ特徴ある入射方向分布を持っていることがわかる。
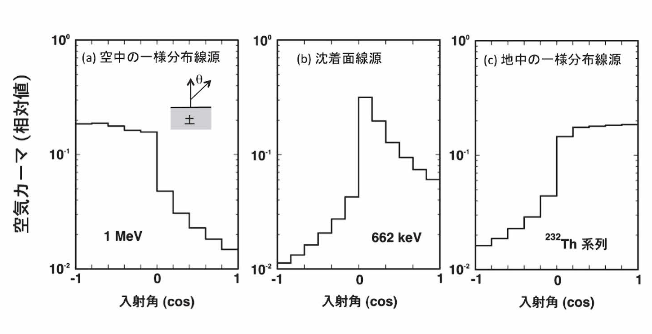
図2 環境中に分布した線源から放出されたγ線による地上1mにおける空気カーマの入射方向分布12)
一様分布体積線源の場合には、線源が存在する半球方向から等方に近いγ線が入射し、線源が存在しない反対の半球方向からは散乱線がわずかに入射する。例えば、図2(a)の空中の一様分布体積線源の場合は、上方の2π方向からやってくるγ線はほぼ等方であり、下方からは土により散乱されたγ線が少量やってくる。上方の2π方向に関しては等方入射(ISO)に近い方向分布をしているが、下方の2πからのγ線に関してはISOとは異なる方向分布をしている。
沈着面線源の場合には、図2(b)に示すように、水平方向から主なγ線成分が入射することがわかる。このような沈着面線源の特徴的な入射方向分布は、図3(a)を参照しながら立体角あたりの線源の量を考えると理解がしやすい。すなわち、地上1mの検出器から線源を見る方向が水平に近づくにつれ、立体角あたりに存在する線源の量が急激に増えることがわかる。
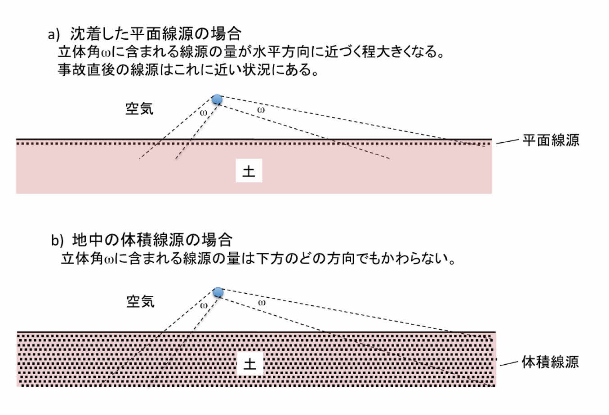
図3 地上1mの検出器から地表面線源と地中一様分有線源を見た時の立体角あたりの線源の量の関係
図3(b)の地中の一様体積線源の場合には、どの方向を見ても線源が無限遠まで存在するため、立体角あたりの線源の量は方向によらず同じということになる。地中に指数関数分布した線源(β=1g/cm2)からの地上1mにおける入射方向分布も計算されており13)、やはり水平方向からの成分が空間線量率に大きく寄与している。沈着線源からのγ線は回転対称入射(ROT)に近い入射方向分布を示すものの、ROTとは異なる特有の分布を持つことがわかる。
線源分布が変化すると、γ線入射方向分布も図2で示した分布から変化する。まず、空中の線源について見てみると、ガウスプルーム線源では空中一様分有線源とは異なる特徴を示す。図4に示すように、プルームの直下においてはγ線が真上方向から、ガウスプルームから離れた地点では横方向から入射する12)。
-
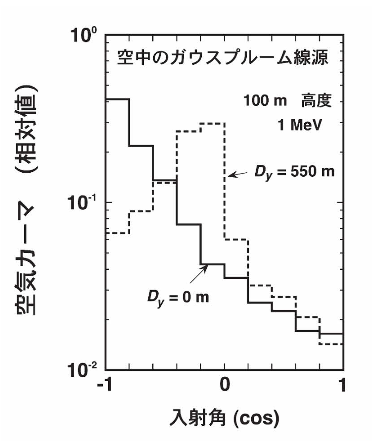
図4 高度100mに存在するガウスプルーム線源の直下( D y=0m)及びプルーム軸から直交距離550mの地点( D y=550m)におけるγ線の入射方向分布12)大気安定度はF、風下距離は750mを想定している。
-
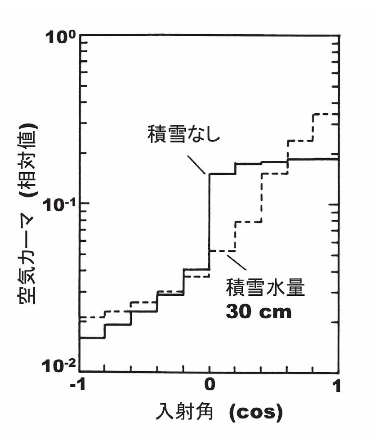
図5 積雪による地殻γ線の入射方向分布の変化 232Th系列核種が地中に一様分布している場合の結果を示す。
地中の指数関数分有線源については、緩衝深度βが増えるにつれて、水平からの成分が徐々に小さくなり、βが無限となる体稜線源では、図2(c)に示すように、下方から等方的にγ線が入射するようになる。また、地中一様分有線源の上に積雪があった場合には、斜め方向からのγ線が遮蔽され、図5に示すように下方からの成分が大きくなる14)。このように、環境γの入射方向は、環境中の線源分布や状況により様々に変化する性質を持つ。
2.2.2 エネルギー分布
図6は地中の様々な深さに存在する137Cs平面線源からのγ線による地上1mにおける空気カーマのエネルギー分布を示している15)。線源が浅い位置にある場合には直接線の寄与が大きく、線源の深度が増すにつれ散乱成分の割合が増加する。すなわち、662keVのγ線のピークが低くなり、環境中で散乱された低いエネルギーのγ線の平らな部分が高くなる。
-
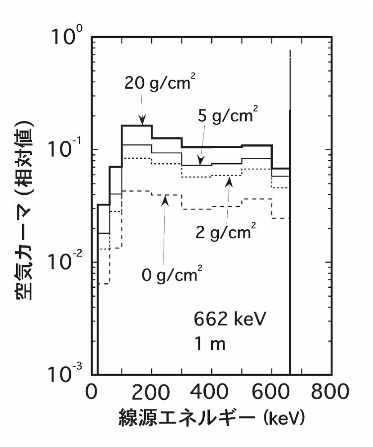
図6 地中の異なる深さに存在する137Cs平面線源からのγ線による地上1mにおける空気カーマのエネルギー分布15)
-
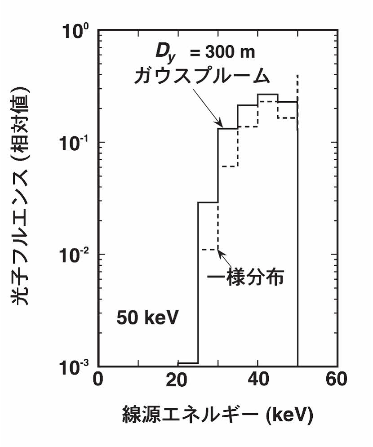
図7 50keVのγ線を放出するガウスプルーム線源並びに一様分有線源からのγ線による地上1mにおける光子フルエンスエネルギー分有の違い12)ガウスプルーム線源については放出高100m、大気安定度Fを想定し、風下距離が750m、直交距離が300mの地点でのフルエンスを示している
空中の線源の場合でも、一様分布体積線源では直接線が大きな割合を占めるが、ガウスプルーム線源においてプルームからの距離が大きくなるにつれて散乱線の割合が増加する。図7では、50keVのγ線を放出する線源が空中に一様分布する場合と、ガウスプルーム分布をする場合についてγ線フルエンスのエネルギー分布を比べている10)。ガウスプルームに関しては、放出高100m、大気安定度Fを想定し、プルーム軸から300m離れた地点のデータを表しているが、明らかなエネルギー分布の違いが見られる。空中の一様分布体積線源の場合には、線源から直接にやってくる50keVのγ線の寄与が大きいのに対し、ガウスプルーム線源では、50keV以下の散乱線の割合が大きくなる。
2.3.3 高度変化
空間線量率の地上高度による変化の様子は線源分布により大きく異なる。図8は、地中に指数関数分布した137Cs線源から放出されるγ線による空間線量率が高度によりどのように変化するか、シミュレーションにより調べた結果である16)。緩衝深度βが異なる3種類の指数関数分布に対する空間線量率の高度変化を示しているが、βが小さな場合、すなわち地表面付近に集中して放射性物質が存在する場合は、高度とともに急激に空間線量率が減少する。βが大きくなるに従って、すなわち放射性物質が地中に広く分布するに従って高度変化が緩やかになる。
地表面近くに沈着した線源においては、2.2.1でみたように水平方向からやってくるγ線が大きな割合を占める。高度が増すと、水平方向からやってくるγ線が通過する空気の距離が急に増えることになり、空気による遮蔽の影響も急激に増加する。そのために水平からの成分が減少し空間線量率全体も減少することになる。
福島事故による放射性物質が沈着した場所においては、地表面で測定した空間線量率と地上1mの空間線量率が明らかに異なることがよく知られているが、これは事故による放射性核種が沈着した地点の特徴である。地中に一様分布した天然放射性核種の場合は、このような顕著な高度変化はみられない。
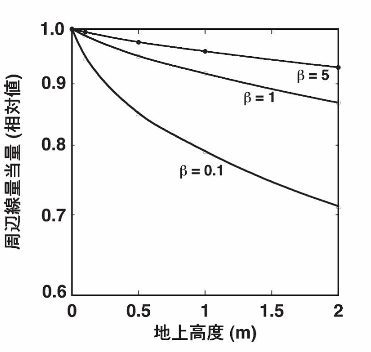
図8 地中に指数関数分布する線源による周辺線量当量の地上高度による変化16)異なる緩衝深度β(g/cm2)を持つ3種類の線源に対し、それぞれのケースで地表面における周辺線量当量を1として相対値を示した。
なお図8においては、地表面の空間線量率を1とした時の相対的な線量率高度変化をそれぞれの緩衝深度に対して表している。もし沈着量(Bq/m2)が同じであれば、緩衝深度βが大きい程、空間線量率の絶対値は小さくなることに注意していただきたい
3. 環境γ線からの被ばく線量の評価
Ⅱで説明したように、人間の外部被ばく線量はγ線の入射方向とエネルギー分布により様々に変化する。したがって、環境中における被ばく線量を現実的に評価するためには、環境γ線特有の人体への入射方向分布やエネルギー分布を考慮して人間の被ばく線量を求める必要がある。
このための研究が、ファントムと呼ばれる人体モデルとモンテカルロシミュレーションを用いて以前から行われてきた。ここでは、最近公表された成果6),7)を中心に、必要に応じて過去の研究も参照して環境中における被ばく線量について議論する。
3.1 シミュレーションモデル
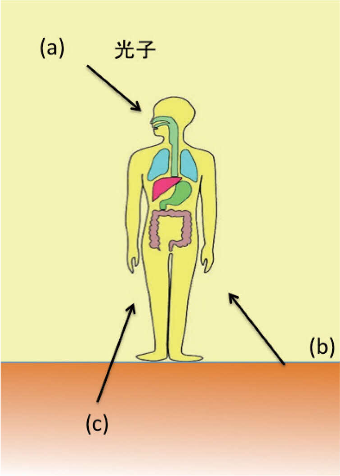
図9 環境中における被ばくシミュレーションの概念図
図9は典型的な環境線源に対する被ばくシミュレーションの概念図を示す。(a)空中の一様分布体積線源、(b)0.5g/cm2の深さに存在する一様分布した面線源(沈着面線源)、(c)地中の一様分布体積線源の3種類の線源が考慮されている。(a)は施設から放出された放射性核種が空中に留まっている場合を、(b)は空中にあった放射性核種が地表に沈着した直後を、(c)は天然放射性核種をそれぞれ想定している。
(a)と(b)については様々な単色エネルギー線源に対するシミュレーションを最初に行い、その後に核データを用いて放射性核種ごとの線量換算係数を求めている。(b)では地面の凹凸の影響及び放射性核種の初期浸透を考慮して0.5g/cm2の深さの平面線源を考えている。(c)では238U系列核種、232Th系列核種から放出される主要なγ線及び40Kから放出される1.46MeVγ線をそれぞれ考えている。2章で見た環境γ線特有の性質を詳細に考慮し3)、最新の人体モデルを用いて被ばく計算が行われた6)。
被ばくを受ける人体は地表面に直立している状況を想定し、成人に加え年齢の異なる子供の被ばくも考えている。成人については、放射線防護の被ばく線量評価で標準とされる、平均的な体格を持った西欧人の数値人体モデルAM(男性モデル)とAF(女性モデル)が用いられた。AMとAFはCT画像に基づいて作成された、実際の人体に非常に近い構造を持ったモデル(ボクセルファントム)であり17),18)、ICRPにより標準ファントム(reference phantom)として指定されている5)Ⅱを参照のこと)。さらに、ドイツ環境健康研究センター(German Research Center for Environmental Health)で開発された複数の子供のファントム3体19)を用いたシミュレーションも行われた。
3.2 空中一様分有線源と沈着面線源
空中に一様分布した線源及び地中の0.5g/cm2の深さに存在する平面線源から人間が受ける実効線量を図10と図11に示す6)。この図では、地上1mの空気カーマで規格化された実効線量を、環境中線源のエネルギーの関数として表している。また、地上1mの周辺線量当量 H *(10)のエネルギー依存性も同じ図に示している20)。
-
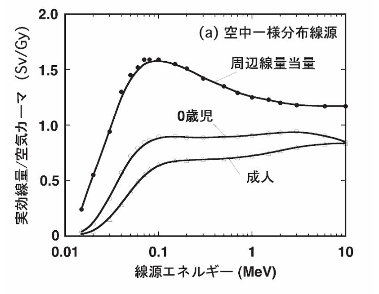
図10 空中の一様分有線源からのγ線により地面に直立した人間が受ける実効線量6)並びに地上1mの周辺線量当量20)
-
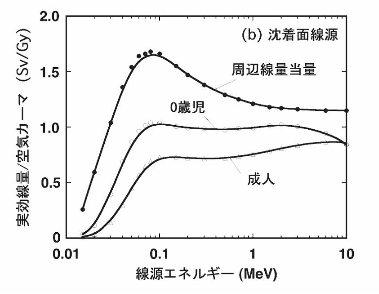
図11 地中の0.5g/cm2の深さに存在する平面線源からのγ線により地面に直立した人間が受ける実効線量6)並びに地上1mの周辺線量当量20)
環境放射線測定においては、地上1mにおける空間線量率が標準的な値として用いられてきた。空間線量率の測定は、周辺線量当量(Sv)あるいは空気カーマと実質的に等価な空気吸収線量(Gy)により行われる。したがって、図10、11の関係を用いれば、環境における空間線量率測定値から実効線量率を評価することができる。もし、環境線源から放出されるγ線エネルギーが単色であれば、空間線量率(Gy/h、Sv/h)に図に示された比率を掛けることで実効線量率(Sv/h)を求めることができる。
成人と乳児の実効線量を比較するといずれの線源の場合も乳児の線量が大きいことがわかる。これは前述したように、人体による自己遮蔽効果が乳児の場合小さく、γ線が臓器・組織に大きなエネルギー付与をするためである。また、沈着面線源の場合は線量率が高度により変化する効果も加わっている。被ばく線量の大きさは一般的に体が大きいほど被ばく線量は小さくなるため、成人と乳児の間のいかなる年齢の子供も、図10と11に示された成人と乳児の間の線量となる。
空中一様分有線源と沈着面線源からの実効線量を比べると、沈着面線源のほうが実効線量が少し大きな値を示す。前章で見たように、沈着面線源の場合は、γ線が水平方向から主に入射し、水平方向からのγ線に対して人体は自己遮蔽効果が小さいためにこのような差が現れる。ただし、その差はそれ程大きくない。
図に示された単色エネルギー線源に対する実効線量のエネルギー依存性をもとに、ICRPの標準核データ21)として採用された最新の核データ22)を参考にして、放射性核種の環境中濃度から実効線量を求めるための線量換算係数が得られている。例えば、沈着面線源の場合、沈着量(Bq/m2)から地上1mの空気カーマ率(Gy/h)を計算する換算係数に図11に示された実効線量への換算係数(Sv/Gy)を掛け、さらにγの放出割合、また複数のγ線が放出される放射性核種であれば、全ての放出γ線を核データに基づいて考慮することで、沈着量(Bq/m2)から実効線量率(Sv/h)を求める換算係数が得られる。
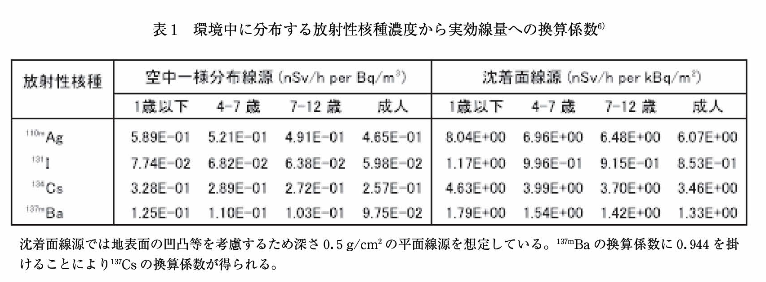
福島事故で観測された重要な沈着放射性核種に対する係数を表1にまとめる。このデータからわかるように、主要な核種に対して成人と乳児の実効線量の違いは40%以内である。この表に示された137mBaは137Csが壊変してできる核種で、0.662keVγ線は正確には137mBaから放出される。137mBaの線量換算係数に0.944を掛けることで137Csの線量換算係数を得ることができる。他の放射性核種に対するデータは元の論文を参照いただきたい6)。
3.3 地中の指数関数分布線源
上記のシミュレーションの結果をもとにして、地中の指数関数分有線源に対する被ばく線量の評価も行われた7)。
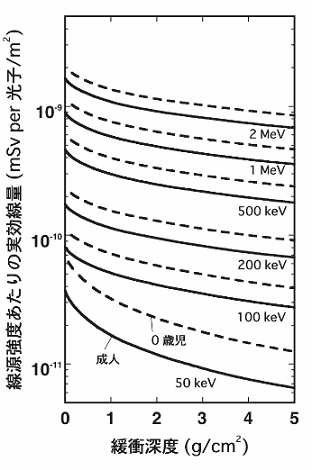
図12 地中の指数関数分布線源からのγ線により地面に直立した人間が受ける実効線量の緩衝深度による変化7)
図12は、単色エネルギーのγ線を放出する指数関数分有線源からの実効線量が、緩衝深度βによりどのように変化するかを示している。線源エネルギーが150keV以上の領域では、地表面の平面線源(β=0g/cm2)に比べてβ=5g/cm2の場合、沈着量あたりの実効線量は約40%に減少する。これは、土によるγ線遮蔽効果が増すためである。ただし、β=5g/cm2になるには普通の環境状況では5年以上を要する。ちなみに、事故から2年9か月が経過した時点での福島周辺における実効的なβは約2.6g/cm2であることが多数の測定結果から明らかにされている23)。
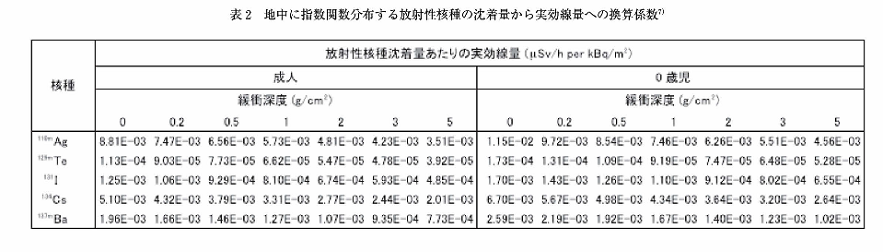
単色エネルギーγ線に対する実効線量をもとに計算した、主要な放射性核種に対する実効線量換算係数を表2にまとめる。この表の値を使えば、放射性核種の沈着量から成人及び乳児の実効線量を評価することが可能である。他の放射性核種や緩衝深度に対する詳細なデータは文献7)を参照のこと。
3.4 地中の天然放射性核種線源
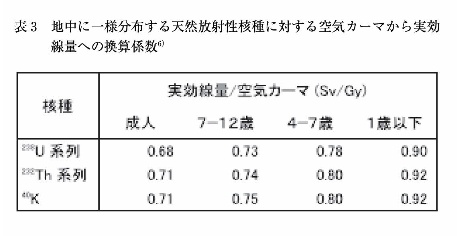
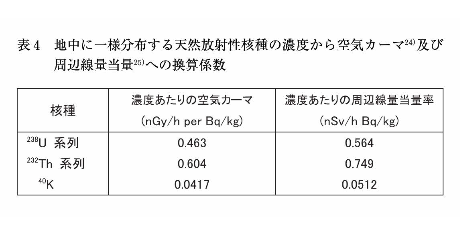
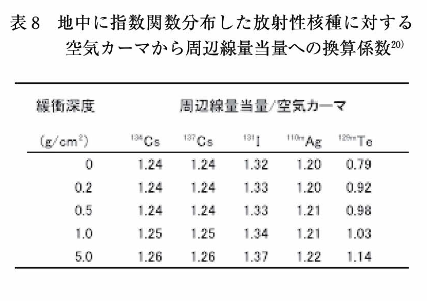
地中に一様分布する天然放射性核種(238U系列核種、232Th系列核種、40K)による実効線量と空気カーマとの関係を表3に示す。空気吸収線量で重み付けされた、地上1mにおけるγ平均エネルギーはこれら天然放射性核種間で似通っているため、空気カーマから実効線量への換算係数(Sv/Gy)も近い値が得られる。成人の場合は0.7程度、乳児の場合には0.9程度である。地中の天然放射性核種濃度(Bq/kg)から地上1mの空気カーマ率(Gy/h)を計算するための換算係数が与えられているため、地中の天然放射性核種の濃度から実効線量率を計算することも可能である。表4には、地中の238U、232Th、40Kの濃度から空気カーマを計算するための換算係数24)、並びに周辺線量当量を計算するために換算係数25)を一緒に示す。
3.5 環境中における実効線量の変動
環境中における実効線量は様々な要因で変動する。被ばく線量評価を行う時に実効線量の変動要因とその程度を把握しておくことは重要である。以下に、主な変動要因とその程度についてまとめる。ここで議論するのは、サーベイメータで空間線量率を測定した値が同じでも条件により実効線量がどの程度変化しうるかということに相当する。
3.5.1 年齢による変動
実効線量と体格の関係について体重をパラメータとして近似的に表すと、体重の立方根に反比例して指数関数的に線量が小さくなることが明らかにされている26)。乳児の実効線量を成人と比べた場合に、環境中での被ばくで主に問題なる50keV以上のγ線に対しては、最大でもその違いは2倍以内、エネルギーが高いγに対しては数10%程度である。ちなみに地表面に沈着した放射性セシウムの場合は、表2を参照すると、乳児の実効線量は成人より30%程度、低エネルギーγ線を放出する129mTeの場合は50%程度大きくなる。
体重の関数を使って年齢ごとの実効線量を概算してみると、0歳から1歳までに相対的に遠く実効線量が減少し1歳から12歳までは年齢に反比例して線量が減少すること、12歳の実効線量は成人の実効線量にかなり近いこと等がわかる26)。
3.5.2 人種、体格の個人差による変動
放射線防護の基準とされる実効線量は西欧標準人を対象に評価される。西欧人に対して用意された線量評価データをそのまま日本人に適応してよいのだろうかという疑問が、直ぐに頭に浮かぶと思う。結論から述べると、西欧人と日本人との体格の差は、環境中の外部被ばくにおいては、大きな影響は与えない。
人種による被ばく線量の違いを明らかにするため、日本人のCT画像データに基づく詳細な人体モデルが開発され、いろいろな条件に対して線量計算を実施して西欧人との比較が行われた。この結果によれば、γ線が全方向から人体に入射する等方入射(ISO)や回転対称入射(ROT)の場合の実効線量に関しては、西欧人と日本人の差は非常に小さいことがわかっている27)。
また、同じ成人でも痩せた人から太った人まで様々な体格の人間が存在するが、体格の個人差が被ばく線量に与える影響も気になるところである。個人の体重差を広い範囲で変動させて行った解析によれば、体格の個人差の影響も大きくない26)。また、文献6)においては、体重が103kg ある大柄な人間のボクセルファントムを使用したシミュレーションを行いICRPの標準人の結果と比較しているが、線源エネルギーが50keV以上で20%以内、100keV以上では10%以内で実効線量が一致することがわかった。
これらを総合すると、西欧標準人に対して用意されたデータを用いれば、環境中の日本人人の外部被ばくは一般に10%程度の不確かさで評価することができることになる。これは、実効線量の性質を考えれば十分な精度である。
3.5.3 その他の条件による変動
(1) 線源分布の偏りの影響
原子力施設から放出された放射性物質がガウスプルームに近い分布をすることは前に述べた。ガウスプルームから放出されたγ線による実効線量と空気カーマの比率(Sv/Gy)の場所による変化を表5にまとめた12)。
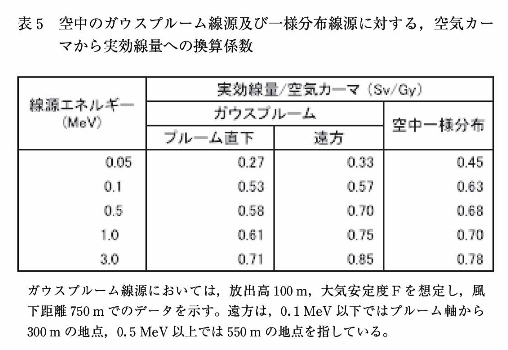
ここでは、ガウスプルーム線源の直下と離れた位置とでSv/Gyがどのように変化するかを、様々な線源エネルギーに対してシミュレーションにより求めた結果である。プルームの放出高は100m、大気安定度はF、風下距離は750mの地点における値を示した。
エネルギーが500keV以上の場合、ガウスプルームの直下においてはγ線の入射方向が真上方向に偏るため、自己遮蔽効果の増加により被ばく線量は空中の一様分有線源に比べて小さくなる。一方、ガウスプルームから離れた地点では、入射方向が水平方向に近くなるため、被ばく線量が大きくなる傾向にある。しかしその変動の程度は10%程度である。一方、100keV以下のエネルギーでは、プルームの直下でも離れた位置でも、Sv/Gyは一様分布線源に比べて小さくなる。これは、エネルギー分布が低いほうへ変化するために、図10に示したGyとSvの低エネルギーにおける差が大きく反映されるためである。
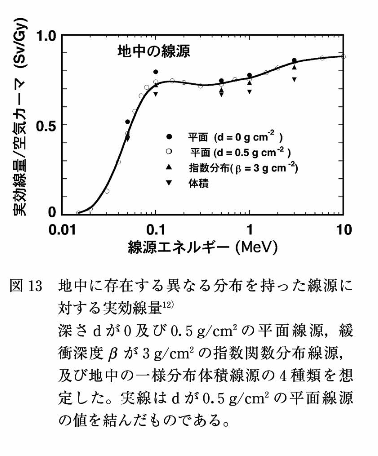
地中に分布した線源に対する実効線量と空気カーマの関係(Sv/Gy)を図13に示す12)。ここでは、①地表面の平面線源、②地中0.5g/cm2の深さに存在する平面線源、③緩衝深度β=3g/cm2の指数関数分布線源、④一様分布体積線源を想定し、実効線量と空気カーマの関係を計算している。Sv/Gyの比率は、②地中0.5g/cm2の深さに存在する平面線源の係数により、ここで考えた全ての線源の係数を15%以内の誤差で評価することが可能である
(2) 人体の姿勢の影響
人体が地表面に直立していることを想定して基本的な被ばくシミュレーションが行われているが、環境中で人間は常に直立している訳ではない。人間が横たわった時の被ばく線量の変化もシミュレーションにより調べられ、人体の姿勢の影響について解析が行われた12)。
14a)とb)は、人間が仰向けあるいはうつ伏せの姿勢をとった時に、立位と比べて実効線量がどのように変化するかを示している。空中の一様分布線源の場合、仰向けの状態では直立に比べて実効線量が高く、逆にうつ伏せの状態では低くなる。被ばく上重要な臓器・組織は人体の全面に多く存在する傾向があるため、線源の方向に人体を向けた仰向けでは実効線量が高くなる。
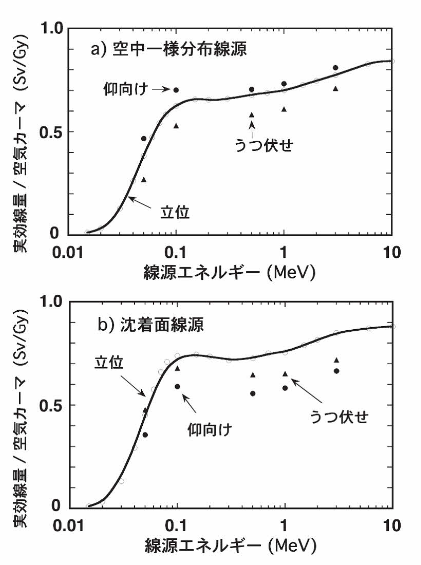
図14 人体の姿勢による実効線量の変化12)
a)空中の一様分有線源、及びb)沈着面線源(深さ0.5g/cm2)を想定し、仰向けとうつ伏せの姿勢をとった時に、実効線量が立位に比べてどの程度変化するかを示している。
しかし、地表面線源の場合には、うつ伏せでも仰向けでも実効線量は小さくなる。水平方向から主要なγ線がやってくるため、直立した状態では自己遮蔽効果が小さく、実効線量が大きくなるのに対し、横たわった状態では人体平面を取り囲む円周方向からγ線が入射するため自己遮蔽が大きくなり、うつ伏せでも仰向けでも線量が大きくなる。
人体姿勢による実効線量の変動は最大で20~30%程度存在する。しかし、地表面線源の場合は、直立状態に対して実効線量を評価しておけば、安全側(過大評価側)に被ばく線量を評価することが可能である。したがって、福島周辺での被ばくでは、直立した状態での線量換算係数を用いれば、安全側の評価が可能である。
4. 空間線量率の測定値と被ばく線量の関係
空間線量率から生活時同等について単純な仮定をおいて推定した被ばく線量と、個人線量計を装着して測定した被ばく線量の値に大きな違いが見られることが報告されている。別の号で詳細に議論するように、この被ばく線量の食い違いにはいくつかの原因が考えられるが、一つの基本的な原因として空間線量率測定に用いられている線量(周辺線量当量、空気吸収線量)と、被ばく線量評価に用いられる線量(実効線量)の関係を正しく考慮せずに評価が行われている場合があることが挙げられる。
福島事故で検出された主な沈着放射性核種に対する、周辺線量当量から実効線量への換算係数を表6に、空気吸収線量(空気カーマ)から実効線量への換算係数を表7にそれぞれ示す。
周辺線量当量は作業環境における空間線量率を安全側に評価するために導入された量であり、自然環境で用いた場合には図10と図11に示したように、実効線量を必要以上に大きく過大評価してしまう傾向にある。
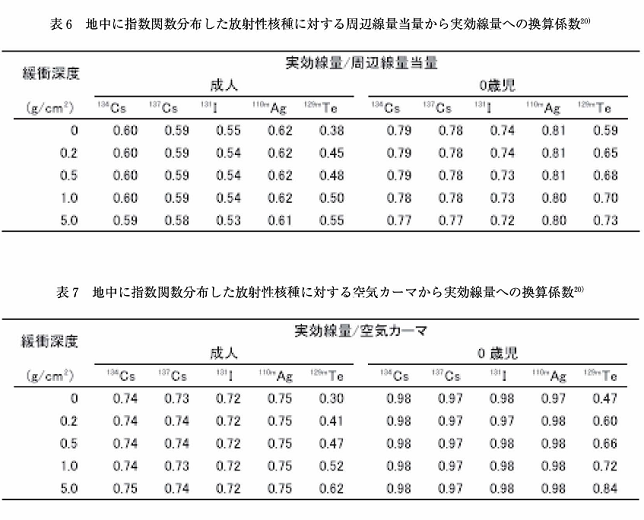
具体的な放射性核種に関する数字を示すと、放射性セシウムが沈着した場においては、表6に示すように、成人の実効線量は周辺線量当量のほぼ60%である。線源エネルギーが小さい場合には差はさらに大きくなる。例えば、131Iの場合には実効線量は周辺線量当量の55%になる。また、周辺線量当量は0歳児の実効線量も20%以上過大評価することになる。
空間線量率の測定にどのような線量を用いるのが適切なのかを考えた場合、実効線量の評価の観点からは、空気吸収線量(空気カーマ)を用いるほうがより適切と考えられる。空気吸収線量では、図10と図11並びに表7に示すように、乳児の線量も含めて実効線量を安全側に評価することができ、しかも、周辺線量当量のように過度に過大評価をすることがない。また、エネルギー特性も実効線量に近い形をしているため、広いエネルギー範囲の線源に対して、適切な被ばく線量の評価が可能である。表7に示すように、実効線量と空気カーマの比率が放射性核種によりほとんど変化しない。したがって、空気カーマを測定しておけば核種によらず少ない誤差で実効線量を評価できることになる。
一方、空間線量率は施設内でも環境中でも共通の線量を用いて行うべきとの考え方に基づいて、周辺線量当量を用いた環境中の空間線量率測定が国際的にもまた日本国内でも広く行われてきたのが実情である。したがって、本稿で説明した周辺線量当量と実効線量の関係について十分に念頭において、測定結果を眺める必要がある。
福島周辺の多数の地点において、空間線量率を周辺線量当量率と空気吸収線量率の両方で測定し、比較した例が報告されている10)・28)。この結果によれば、放射性セシウムが沈着した地域では、周辺線量当量率と空気吸収線量率の比率(Sv/Gy)は1.25前後であった。この値はシミュレーションにより得られた値(表8の放射性セシウムに対する値)ともよく一致している。なお、地中に分布した天然放射性核種の場合には平均エネルギーが高いことから、周辺線量当量と空気カーマの比率は多少小さくなる傾向にあり、表4のデータを参照すれば、1.2~1.25の間になる。
5. まとめ
実効線量を評価するための基礎データとして、作業環境を想定した単純な入射条件に対する線量換算係数はICRPの報告書等にまとめられ、広く参照されてきた。一方、環境中における被ばくを想定した線量評価用基礎データに関しては、研究自体は相当数行われて成果も蓄積されてきており、UNSCEARの報告書等ではその一部が参照されてきた。しかし、ICRPの報告書の形で集約されることがなかったこともあり、その存在や特徴に関して一般に広くは知られていない。今回の福島事故を契機に、被ばく線量評価上の知識の不足や問題点がいろいろ露呈されてきており、環境中での被ばく線量評価上の論点を整理することが必要とされている。
現在、ICRPはタスクグループTG9030)を立ち上げ、環境に分布した放射性核種に対する公衆の年齢別線量換算係数の整備作業を進めていが、筆者らもこのタスクグループに参加している。ここでは、内部被ばく評価用に開発された年齢別の標準ファントム10体を31)、福島事故を契機に外部被ばく評価へも適用することとし、現在、線量換算係数整備のためのシミュレーション作業を日本原子力研究開発機構の佐藤大樹研究員が中心となり行っている段階である。報告書は2016~17年に発刊の段階である32)。
一方、ICRPの報告書の発刊を待つ間にも、環境中における被ばく線量評価用の基礎データのニーズは大きい。本稿では、これまでの研究結果を参照し、環境中における実効線量の特徴や線量評価のための基礎データの紹介を行った。環境γ線と環境中被ばくに関して、おおまかなイメージを持っていただくとともに、データを活用していただければ幸いである。
本稿で述べた要点をまとめる。
- 環境中における被ばく線量を評価するためには、環境γ線特有の性質を考慮することが必要である。
- 環境γ線による被ばくのシミュレーションはこれまでにある程度行われてきており、環境中被ばくの特徴や線量評価のための基礎デ ータが存在する。
- 周辺線量当量、空気吸収線量(空気カーマ)、並びに環境中の放射性核種濃度から実効線量を評価するための線量換算係数が利用可能で ある。
- 被ばく線量は様々な要因で変動するが、標準的な被ばく評価用のデータを使用すれば、数10%の不確かさで実効線量を評価できる。
- 環境中においては、周辺線量当量は実効線量を必要以上に過大評価する傾向にある。筆者らの意見として、環境中における実効線量の評価を考えた場合には、空間線量率を測定するのに周辺線量当量率よりは空気吸収線量(空気カーマ)率を測定するほうが適当である
参考文献
- United Nations Scientific Committee on the Effects of Atomic Radiation, Source and Effects of Ionization Radiation, Annex J: Exposure and Effects of the Chernobyl Accident, UNSCEAR 2000 Report Vol. II, 2000, 117p.
- 日本原子力学会 放射線工学部界, “測定値(空気中放射線量)と実効線量", 2012-07-26.
- Saito, K. et al, Calculation of organ doses from environmental gamma rays using human phantoms and Monte Carlo methods, Part I; Monoenergetic sources and natural radionuclides in the Ground. GSF-2/90, Gesellschaft fur Strahlen und Umweltforschung mbH Munchen, 1990, 119p.
- Eckerman, K.F. et al, External exposure to radionuclides in air, water, and soil, EPA-402-R-93-081, Oak Ridge National Laboratory, 1993, 238p.
- Valentin, J., The 2007 Recommendations of the International Commission on Radiological Protection, ICRP Publication 103, Annals of the ICRP, vol.37, no.2-4, 2007.
- Petoussi-Henss N. et al, Organ doses from environmental exposures calculated using voxel phantoms of adults and children, Physics in Medicine and Biology, vol.57, no.18, 2012, p.5679-5713.
- Saito, K. et al, Effective dose conversion coefficients for radionuclides exponentially distributed in the ground, Radiation and Environmental Biophysics, vol.51, no.4, 2012, p.411-423.
- 波戸真治ほか, 狭域野外拡散試験データを用いた大気拡散モデルの妥当性の検討, JAEA-Research 2008-094, 日本原子力研究開発機構, 2008, 95p.
- Andersson K.G. et al, Weathering of radiocaesium contamination on urban streets, walls and roofs, Journal of Environmental Radioactivity, vol.62, no.1, 2002, p.49-60.
- 日本原子力研究開発機構, “平成24年度放射能測定調査委託事業「福島第一原子力発電所事故に伴う放射性物質の長期的影響把握手法の確立」成果報告書".
- 1Jacob, P. et al, Gamma-Ray Spectrometry in the environment, ICRU Report 53, Journal of the ICRU, vol.27, no.2, 1994.
- Saito, K. et al, Calculation of the effective dose from environmental gamma ray sources and its variation, Health Physics, vol.74, no.6, 1998, p.698-706.
- 平山英夫, EGS5による地表に広く分布した134Cs及び137Csの環境における個人線量計の評価, Radioisotopes, vol.62, no.6, 2013, p.335-345.
- Saito, K., External dose due to terrestrial gamma rays on the snow cover, Radiation Protection Dosimetry, vol.35, no.1, 1991, p.31-39.
- Saito, K. et al, Fundamental data on environmental gamma-ray fields in the air due to sources in the ground, JAERI-Data/Code 98-001, Japan Atomic Energy Research Institute, 1998, 93p.
- 斎藤公明, 環境中に分布する放射性核種に対する外部被ばく線量評価に関する研究, 名古屋大学博士学位論文, 2013, 102p.
- Zankl, M. el al, GSF male and female adult voxel models representing ICRP reference Man - The present status, The Monte Carlo Method: Versatility Unbounded in a Dynamic Computing World, Chattanooga, TN, USA, 2005-04-17/21.
- ICRP, Adult reference computational phantoms, ICRP Publication 110, Annals of the ICRP, vol.39, no.2, 2009.
- Petoussi-Henss, N. et al, The GSF family of voxel phantoms, Physics in Medicine and Biology, vol.47, no.1, 2002, p.89–106.
- Saito, K. et al, Ambient dose equivalent conversion coefficients for radionuclides exponentially distributed in the ground, Journal of Nuclear Science and Technology, vol.51, no.10, 2014, p.1274-1287.
- Valentin, J., Nuclear decay data for dosimetric calculations. ICRP Publication 107, Annals of the ICRP, vol.38, no.3, 2008.
- Endo, A. et al, Development and assessment of a new radioactive decay database used for dosimetry calculation, Radiation Protection Dosimetry, vol.105, no.1-5, 2003, p.565–569.
- 原子力規制委員会, “平成26年度東京電力株式会社福島第一原子力発電所事故に伴う放射性物質の分布データの集約及び移行モデルの開発事業成果報告書", 2015.
- Saito, K. et al, Gamma ray fields in the air due to sources in the ground, Radiation Protection Dosimetry, vol.58, no.1, 1995, p.29-45.
- Lemercier, M. et al, Specific Activity to H*(10) Conversion Coefficients for In Situ Gamma Spectrometry, Radiation Protection Dosimetry, vol.128, no.1, 2008, p.83-89.
- Saito, K. et al, Organ doses as a function of body weight for environmental gamma rays, Journal of Nuclear Science and Technology, vol.28, no.7, 1991, p.627-641.
- Sato, K. et al, Dose conversion coefficients calculated using a series of adult Japanese voxel phantoms against external photon exposure, JAEA-Data/Code 2008-016, Japan Atomic Energy Agency, 2008, 173p.
- 日本原子力研究開発機構, “平成23年度放射能測定調査委託事業「福島第一原子力発電所事故に伴う放射性物質の第二次分布状況等に関する研究調査」 成果報告書」", 2013.
- 日本原子力研究開発機構, “平成24年度放射能測定調査委託事業「福島第一原子力発電所事故に伴う放射性物質の長期的影響把握手法の確立」成果報告書".
- ICRP, “Task Group 90; Age-dependent Dose Conversion Coefficients for External Exposures to Environmental Sources"
- ICRP, “Task Group 96; Computational Phantoms and Radiation Transport"