環境動態に関する解析的研究
1. 概要
解析的研究の目的は、調査から推定された現象を演繹的に確認するとともに、将来の環境中の放射性セシウムや線量率の分布を予測し、必要な対策を検討することである。モデルにおいて過去のモニタリング結果を統計処理することで将来に外挿するという統計的アプローチが存在する。しかし、本プロジェクトでは除染や移行抑制などの対策の効果を評価、予測することも視野にしており、統計的アプローチではそれらに対応することは困難である。そのため、本プロジェクトでは現象論的なモデリングアプローチを主としている。
森林内では放射性セシウムは樹木、落葉層、土壌層の中で循環を生じ、一部は山菜や野生鳥獣類などに取り込まれ、一部は河川に流出する。河川やダム湖では浮遊物質に付着した状態あるいは溶存態として流下し、一部は河床・湖底あるいは河川敷に堆積し、あるいは再浮遊し下流へ移行する。土壌中では表層付近に沈着した放射性セシウムが時間とともに緩やかに深部に移行し、そのために空間線量率が物理減衰以上に低下する。解析的研究では、このような森林や陸地での放射性セシウムの挙動、森林・陸地から河川、ダム湖を経由して海に至る過程を網羅的に対象としているが、全ての現象を網羅的に表現する唯一のモデルを開発することは困難であり、また、本来モデル化という行為は簡素化により現象の本質を浮き彫りにすることであることを考えると、過度に複雑なモデル化は好ましくないため、強みの異なる複数のモデルを開発・整備し、検討する課題の規模や現象に応じてモデルを使い分けることとしている。また、将来予測や対策検討の指標として、外部被ばくに対応する線量率、内部被ばくに対応する農林水産物中の放射性セシウム濃度までを対象としている。
解析的研究でこれまで対象としてきた主な課題は、
- 中長期的な放射性セシウム分布、空間線量率分布の評価
- 河川から海に流出する放射性セシウムの流出量の評価
- 大雨時の放射性セシウムの河川、ダム湖での挙動の評価、放射性セシウムの堆積による線量率変化の評価
- 生物利用性の高い溶存態放射性セシウムの挙動の評価
- 環境中の放射性セシウムの動態が農林水産物中の放射性セシウム濃度に与える影響の評価
である。これらの課題に対応すべく、これまでに整備してきた主な解析モデルを図1および表1に示す。
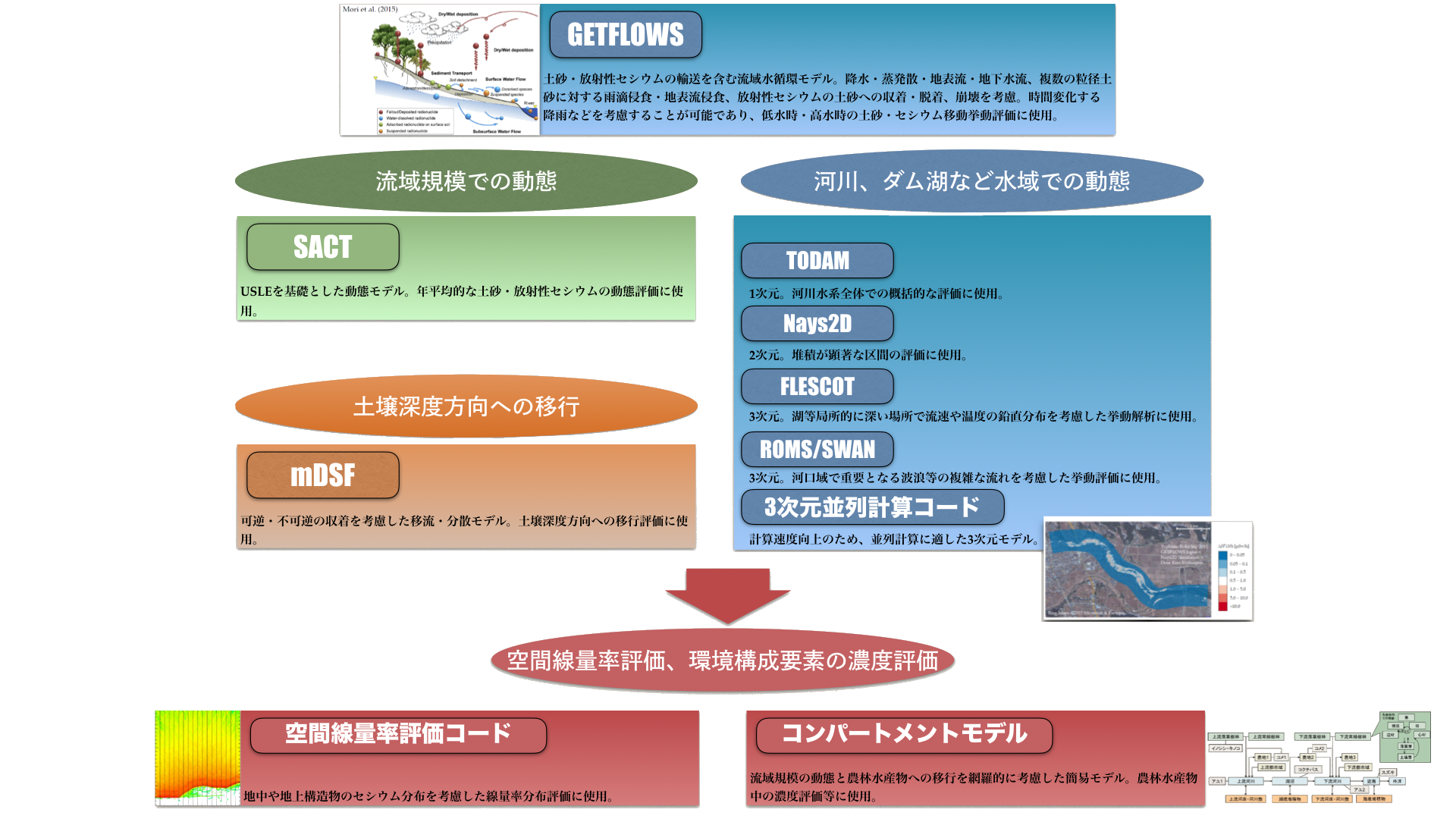
図1 解析モデルと適用範囲
| モデル名 | 概要・適用例 | 開発者 | 参考文献 |
|---|---|---|---|
| 陸域動態モデル | |||
| SACT (Soil And Cs Transport model) | 土壌流亡式USLE (Universal Soil Loss Equation)を基にしたモデル。広域スケールを対象に、地表での土壌侵食およびそれに付随する放射性セシウムの年間規模の動態を解析する。 | JAEA | 山口ほか(2013), Yamaguchi et al. (2014), Kitamura et al. (2014) |
| GETFLOWS (GEneral purpose Terrestrial fluid-FLOW Simulator) | 降水・蒸発散、地表水-地下水流動、土壌の侵食・堆積、放射性セシウム動態を備えた流域循環3次元有限差分プログラム。大雨など短期的な流出挙動を解析する。 | 株式会社地圏環境テクノロジー | Tosaka et al. (2000), Mori et al., (2015) |
| 水域動態モデル | |||
| TODAM (Time-dependent, One-dimensional Degradation And Migration model) | 1次元有限要素プログラム。粒径の異なる3成分の土壌、溶存および土壌に付着する放射性セシウムの河川・湖沼での動的挙動を解析する。 | 米国パシフィックノースウェスト国立研究所(PNNL) | Onishi et al. (2007, 2014a) |
| iRIC/Nays2D | 2次元有限差分プログラム。河川・湖沼の土壌の動的挙動を解析する。湖底や河川敷への空間的な堆積量評価を解析する。 | 北海道大学 | Shimizu (2003), Shimizu et al. (2012) |
| FLESCOT (Flow, Energy, Salinity, Sediment Contaminant Transport model) | 3次有限体積プログラム。粒径の異なる3成分の土壌、溶存および土壌に付着する放射性セシウムの湖沼・河口での動的挙動を解析する。 | 米国パシフィックノースウェスト国立研究所(PNNL) | Onishi et al. (1993, 2014b) |
| ROMS (Regional Ocean Modeling System) | 自由水面、地形追従、プリミティブ方程式群を備えた海洋モデル。科学コミュニティの中で様々な分野で利用されている。河川から週出した放射性セシウムの河口での挙動を解析する。 | ROMSコミュニティ | e.g. Haidvogel et al. (2000) |
| JAEAモデル | 高速・大規模計算を視野に開発中。 | JAEA | |
| 深度移行モデル | |||
| mDSF (modified Diffusion-Sorption-Fixation model) | 放射性セシウムの1次元深度方向移行モデル。有限要素法。土壌への時間遅れを伴う可逆・不可逆的な収脱着を考慮した移流・分散を解析する。 | JAEA | Kurikami et al. (2017) |
| 線量評価モデル | |||
| PHITS (Particle and Heavy Ion Transport code System) | あらゆる物質中での様々な放射線挙動を核反応モデルや核データなどを用いて模擬するモンテカルロ計算コード。環境中の線量率分布の評価を解析する。 | JAEAほか | Sato et al. (2018) |
| ADRET (Air Dose Rate Evaluation Tool) | 平坦な地形において、土壌中の任意の放射性セシウム分布に対して空間線量率を解析する。線量換算係数をPHITSにより算出。 | JAEA | Malins et al. (2016a) |
| 3D-ADRES (3D-Air Dose Rate Evaluation System) | 起伏のある地形や、建物・樹木など地上構造物などジオメトリモデルを作成し、PHITS入力データを構築するシステム。 | JAEA | Kim et al. (2018) |
| 線量評価モデル | |||
| CMFW (Compartment Model for Forest and Water) | 農林水産物への移行を考慮した流域規模の動態コンパートメントモデル。流域規模の放射性セシウムの大局的なマスバランスおよび農林水産物への影響を解析する。 | JAEA | 操上ほか(2017) |
モデルは大きく、陸域動態モデル、水域動態モデル、線量率評価モデル、深度移行モデル、農林水産物移行評価モデルに分けることができる。これらのモデルを、目的に応じて選定あるいは柔軟に組み合わせて評価している。例えば、広範囲の放射性セシウム分布、空間線量率分布、海への流出の予測においては陸域動態モデルを利用し、大雨時の土砂・放射性セシウムの動態については陸域動態モデルと水域動態モデルを組み合わせるなどである。
陸域動態モデルは、森林等の陸域から河川・湖沼、海に至る流域規模の放射性セシウムの動態を解析するものであり、USLE (Universal Soil Loss Equation)を基として年間の平均的な動態を解析するSACT (Soil And Cs Transport model)と、大雨時など短期的なイベント時の水・土砂・放射性セシウム動態を詳細に解析するGETFLOWS (GEneral purpose Terrestrial fluid-FLOW Simulator)を整備している。SACTはJAEAが事故後に独自に開発したモデル、GETFLOWSは株式会社地圏環境テクノロジーが開発したモデルである。
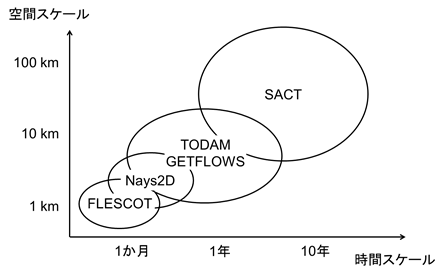
図2 陸水域動態モデルの対象とする時空間スケール(Kurikami et al.(2015)を修正)
水域動態モデルは、河川・湖沼、海の中での水流および土砂、放射性セシウムの動態を解析するものであり、解析対象の時間・空間スケールに応じて1~3次元のモデルを整備している。陸域動態モデルにおいても水域を含めた解析を行うが、陸域動態モデルでは水域の扱いは簡易的であるのに対して、水域動態モデルは水域に特化しており対象とするスケールや精度が異なる(図2)。1次元のTODAM (Time-dependent, One-dimensional Degradation And Migration model)、3次元のFLESCOT (Flow, Energy, Salinity, Sediment Contaminant Transport model)は、PNNL (Pacific Northwest National Laboratory、米国パシフィックノースウェスト国立研究所)が開発したモデル、2次元のiRIC/Nays2Dは北海道大学が開発したモデルである(iRIC/Nays2Dは水流および土砂輸送を解析するが、放射性セシウムの動態は直接的には解析しない)。オープンソースで開発されているROMS (Regional Ocean Modeling System)は海を対象としたモデルであり、SWAN (Simulating Waves Nearshore)を組み合わせることで、波浪および海流を考慮した解析が可能となる。JAEAモデルは、上記の解析ノウハウに基として、高速・大規模計算を視野に開発を進めているJAEA独自モデルである。
深度移行モデルであるmDSF (modified Diffusion-Sorption-Fixation model)は、放射性セシウムの土壌深度方向への1次元の移行を解析する、可逆・不可逆の収脱着を考慮した移流・分散モデルとして独自に開発したものである。
線量率評価モデルADRET (Air Dose Rate Evaluation Tool)は、平坦な地形において土壌中あるいは地上構造物の放射性セシウム分布に基づき線量率分布を解析するものであり、線量換算係数はJAEAが別途開発しているPHITS(Particle and Heavy Ion Transport code System)を利用している。3D-ADRES(3D-Air Dose Rate Evaluation System)は、起伏のある地形や、建物・樹木など地上構造物などジオメトリモデルを作成し、PHITS入力データを構築するシステムである。
農林水産物移行評価モデルCMFW (Compartment Model for Forest and Water)は、流域規模の放射性セシウム動態と農林水産物を結び付けた簡便なコンパートメントモデルであり、流域規模の放射性セシウムの大局的なマスバランスおよび農林水産物への影響を解析するものである。本プロジェクトで対象とする流域規模の放射性セシウムの環境動態が、農林水産物に与える影響を考慮する目的でJAEAが独自に開発を進めている。
以下の2~7章では各モデルについて個別に概要・結果を記し、8章では複数のモデルを組み合わせた事例を述べる。9章は特にモデル検証の視点で整理し、10章において今後の課題を示す。
対象とする課題(あるいは社会的ニーズ)は、事故からの時間の経過とともに変化してきており、それに応じてモデルの整備・改良を進めてきた。事故直後から4~5年程度は、放射性セシウムの環境中での移動量の多くを支配する土砂に付着する放射性セシウムの挙動の評価に重点を置いてきたが、土砂に付着する放射性セシウムの動態の解明が進むにつれて、除染されない森林を主な発生源とする、生物利用性に影響を与える溶存態放射性セシウムの挙動(有機物や土壌への収脱着挙動)に着眼点をシフトしてきている。また、線量率評価についても、構造物のない平坦な地形環境を対象とした深度と線量率に係る解析や除染効果評価等に係る解析から、詳細な地形、地上構造物を考慮した解析へと高度化を進めている。今後も調査の進展、社会的ニーズの変化に伴って、モデルも柔軟に開発・改良を進める予定である。
2. 流域スケール陸域動態モデル(年平均の動態評価)
2.1 目的
流域スケール陸域動態モデルのうち年平均の動態評価を行うSACTを利用した解析的研究の目的は、主に中長期的な放射性セシウム分布、空間線量率分布の予測、河川から海に流出する放射性セシウムの流出量の評価である。
2.2 手法
SACT (山口ほか、2013; Yamaguchi et al., 2014)は、米国農務省が中心となって開発したUSLEを基として、陸域から河川・湖沼、海に至る流域規模の放射性セシウムの年間の平均的な動態を解析するモデルである。モデル、解析条件、解析結果の詳細は山口ほか(2013)、Yamaguchi et al.(2014)、Kitamura et al.(2014)に譲り、本報告書では概要について記載する。
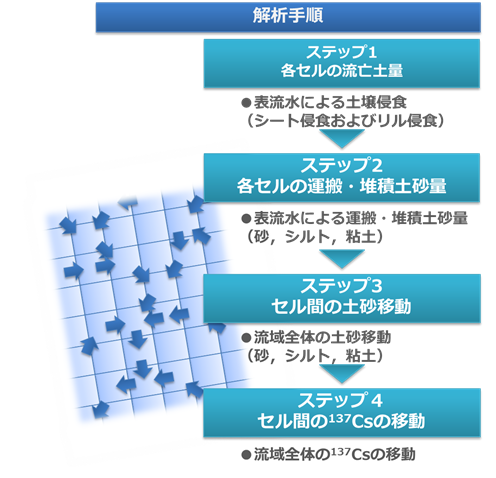
図2-1に示すようにSACTによる計算は主に4つのステップから成っている。
図2-1 SACTの解析プロセス
ステップ1では、東西および南北を100m×100mごとに区切った各セルに対してUSLEを利用し土壌侵食ポテンシャルを計算する。USLEでは、以下の式に示す5つの係数の積により単位面積から1年間に侵食される平均的な土砂の量\( A \) (t ha-1 y-1)を計算する。
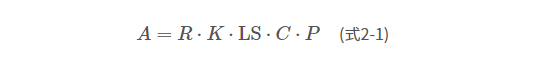
ここで、\( R \) は降水係数、\( K \) は土壌係数、\( LS \) は地形係数、\( C \) は作物係数、\( P \) は保全係数である。各係数は国が提供する降水量、標高データ、土地利用データ、土壌データなどに基づいて設定する。
ステップ2、3では、ステップ1で算出された土壌侵食ポテンシャルのうち、実際に当該セルから下流に移行する土壌フラックスや当該セルでの侵食・堆積フラックスを計算する。SACTにおいては、砂、シルト、粘土の3成分を考慮しているが、非粘着性の砂についてはDu Boys式(Vanoni、1975) により浮遊砂の最大流下容量\( G_{S} \)(t y-1)を算出し、当該セルの上流から流入する砂のフラックス\( Q_{S0} \)(t y-1)、当該セルにおいてUSLEに基づき算出される侵食フラックス\( E_{S} \)(t y-1)を足し合わせたものとの大小関係により、下流への流出フラックス\( Q_{S} \)(t y-1)を算出する(式2-2)。
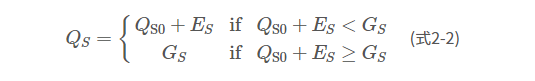
ステップ4では、土砂に付着した137Csの挙動を解析する。土壌中の137Cs濃度プロファイルを指数分布と仮定し、また137Csは全て土壌に付着していると仮定し、砂、シルト、粘土に比表面積に応じて分配する。そして、ステップ3までに計算した粒径ごとの土壌移動に137Csを収着させて計算する。
2.3 結果および考察
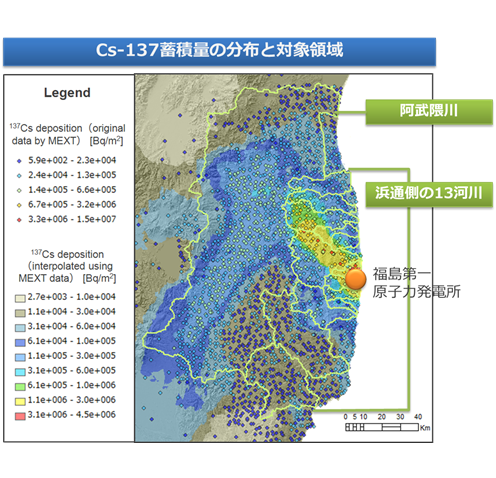
解析対象領域は、阿武隈川、宇多川、真野川、新田川、太田川、小高川、請戸川、前田川、熊川、富岡川、井出川、木戸川、夏井川、鮫川の14流域である(山口ほか、2013; Yamaguchi et al., 2014; Kitamura et al., 2014)。
表2-1に、一年間に各流域から海に流出した土壌および137Csの総量を示す。14河川流域からの流出量は8.4TBqと推察された。なお、これらの値は観測結果に基づく推定値と概ね整合的であることを確認している(Kitamura et al., 2014)が、パラメータの不確実性を考慮した感度解析により0.7~10.2TBq程度にばらつくと想定されている(Yamaguchi et al., 2014)。阿武隈川流域が最も流域面積が広く、そのため土壌、137Csとも流出量は最大となっている。一方、請戸川の流域面積は阿武隈川流域に比べて10分の1以下と小さいものの、137Cs沈着量が多いため137Cs流出量は阿武隈川と大差ない結果となっている。
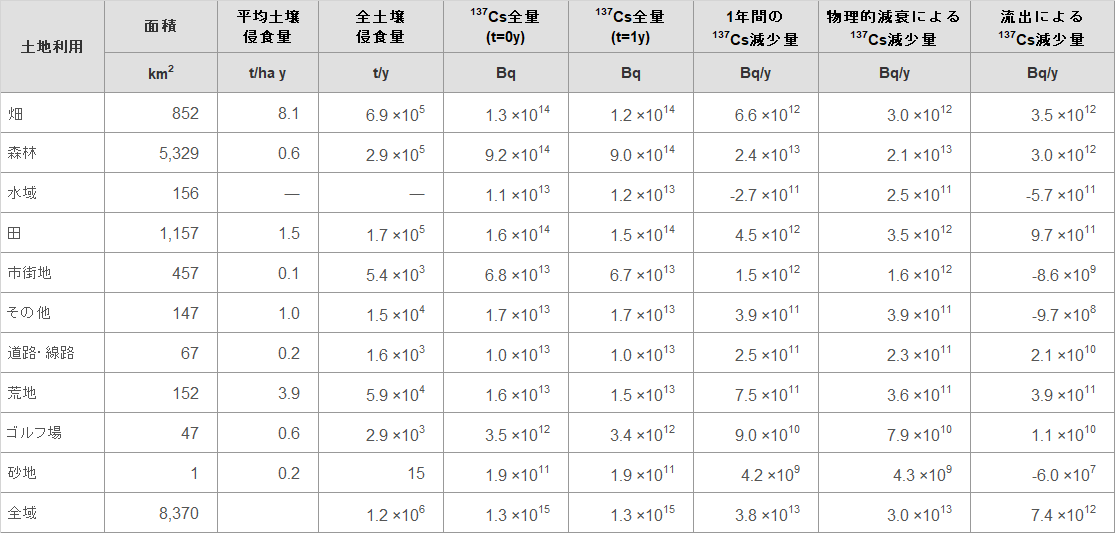
表2-2に、土地利用区分で集計した土壌流出量および137Csの動態を示す。全面積の10%程度に過ぎない畑が、土壌流出量の約58%、放射性セシウム流出量の約47%に寄与している。森林が全面積の64%(森林5,329 km2/全域8,370 km2)を占めるが、土壌侵食量への寄与は24%程度(森林での侵食量2.9×105 t)/全侵食量1.2×106 t)、放射性セシウム流出量への寄与は41%と相対的に小さい。これは森林が樹木や下草、リター層によって被覆されており侵食が抑制されているためである。森林を除染するとこれらの被覆が失われることで荒地になり、土壌・放射性セシウム流出率が上昇する可能性が想定される。なお、森林からの放射性セシウム流出率は年0.3%程度(137Cs流出量3.0×1012 Bq/初期137Cs沈着量9.2×1014 Bq)と見積もられ、この値も実測値と概ね整合的である。
表2-1 一年間に各流域から海に流出した土壌および137Csの総量
| 河川 | 流域面積 (km2) | 海への流出土砂量 (t/y) | 海への流出137Cs量 (Bq/y) | 平均の土砂付着137Cs濃度 (Bq/kg) |
|---|---|---|---|---|
| 阿武隈川 | 5,423 | 2.4 ×105 | 3.0 ×1012 | 1.2 ×104 |
| 請戸川 | 420 | 2.7 ×104 | 2.0 ×1012 | 7.2 ×104 |
| 新田川 | 261 | 1.6 ×104 | 1.1 ×1012 | 6.5 ×104 |
| 前田川 | 48 | 1.6 ×103 | 4.0 ×1011 | 2.5 ×105 |
| 熊川 | 74 | 2.5 ×103 | 2.8 ×1011 | 1.1 ×105 |
| 太田川 | 79 | 1.7 ×103 | 2.7 ×1011 | 1.6 ×105 |
| 真野川 | 167 | 5.5 ×103 | 2.0 ×1011 | 3.7 ×104 |
| 木戸川 | 260 | 1.5 ×104 | 1.4 ×1011 | 9.0 ×103 |
| 小高川 | 67 | 2.5 ×103 | 1.3 ×1011 | 5.3 ×104 |
| 富岡川 | 63 | 2.0 ×103 | 1.1 ×1011 | 5.8 ×104 |
| 夏井川 | 685 | 4.2 ×104 | 1.1 ×1011 | 2.6 ×103 |
| 鮫川 | 592 | 5.1 ×104 | 8.9 ×1010 | 1.7 ×103 |
| 井手川 | 40 | 3.0 ×103 | 6.9 ×1010 | 2.3 ×104 |
| 宇田川 | 173 | 2.4 ×103 | 6.4 ×1010 | 2.6 ×104 |
| 全域 | 8,352 | 4.2 ×105 | 8.4 ×1012 | 2.0 ×104 |
表2-2 土地利用区分ごとの土壌流出量および137Csの動態
SACTによる解析において、いくつかのパラメータは実測値が得られていない、あるいは場所や年とともにばらつきがある。そのため、放射性セシウムの海への流出量の最大値および最小値を算出すること、また影響の大きいパラメータを推定するために、感度解析を実施した(Yamaguchi et al., 2014)。感度解析ケース一覧を表2-3に示す。基本ケースNORMALに対し、変更したパラメータをグレーで網掛けしている。評価対象としたパラメータは不均質性の高いものとし、降水係数(RAIN-1、2)、臨界せん断応力(TAU_C-1、2)、土壌粒径分布(GRAIN)、ダム湖での流速(LAKE_V)、放射性セシウムの緩衝深度(CS_PROF)とした。
表2-3 感度解析ケース
| ケース | 降雨係数 | 臨界せん断応力(砂) | 再浮遊臨界せん断応力(シルト・粘土) | 沈殿臨界せん断応力(シルト・粘土) | 粒径分布(砂:シルト:粘土) | 湖沼での流速 | 137Csの深度分布 | |||
|---|---|---|---|---|---|---|---|---|---|---|
| R(MJ mm ha-1 h-1 y-1) | 河川 τc (Pa) | 陸地 τcr (Pa) | 河川 τcd (Pa) | 陸地 τcd (Pa) | 河川 τcd (Pa) | 陸地 τcd (Pa) | R(%) | Vlake | α(cm-1) | |
| NORMAL | 336.6 | 0.180 | 0.260 | 0.060 | 0.260 | 0.043 | 0.260 | 40:40:20 | 0.01 | 1.20 |
| RAIN-1 | 421.65 | 0.180 | 0.260 | 0.060 | 0.260 | 0.043 | 0.260 | 40:40:20 | 0.01 | 1.20 |
| RAIN-2 | 198.57 | 0.180 | 0.260 | 0.060 | 0.260 | 0.043 | 0.260 | 40:40:20 | 0.01 | 1.20 |
| TAU_C-1 | 336.6 | 0.180 | 7.000 | 0.060 | 7.000 | 0.043 | 7.000 | 40:40:20 | 0.01 | 1.20 |
| TAU_c-2 | 336.6 | 0.180 | 0.260 | 1.300 | 0.260 | 0.800 | 0.260 | 40:40:20 | 0.01 | 1.20 |
| GRAIN | 336.6 | 0.180 | 0.260 | 0.060 | 0.260 | 0.043 | 0.260 | 40:50:10 | 0.01 | 1.20 |
| LAKE_V | 336.6 | 0.180 | 0.260 | 0.060 | 0.260 | 0.043 | 0.260 | 40:40:20 | 0.20 | 1.20 |
| CS_PROF | 336.6 | 0.180 | 0.260 | 0.060 | 0.260 | 0.043 | 0.260 | 40:40:20 | 0.01 | 0.50 |
| MAX | 421.65 | 0.180 | 0.260 | 0.060 | 0.260 | 0.043 | 0.260 | 40:40:20 | 0.20 | 0.50 |
| MIN | 198.57 | 0.180 | 7.000 | 1.300 | 7.000 | 0.800 | 7.000 | 40:50:10 | 0.01 | 1.20 |
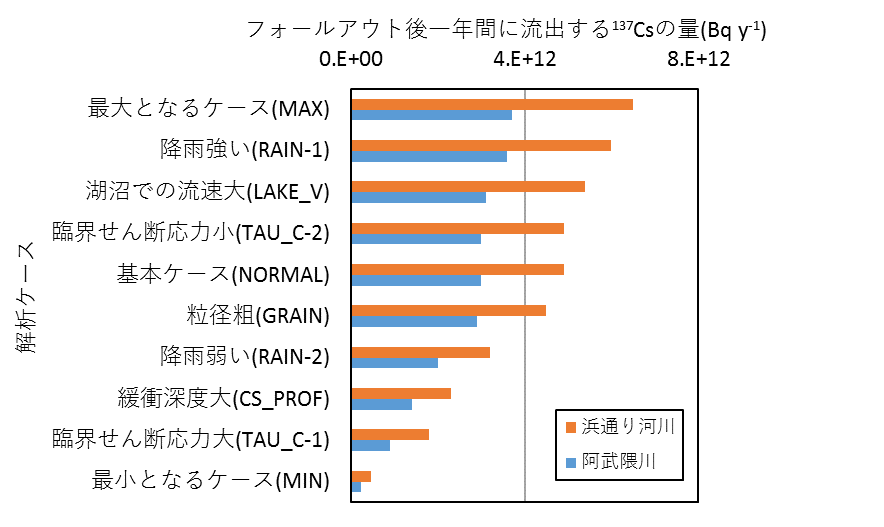
図2-2 感度解析により算出された各ケースでの137Csの海への一年間の流出量
(Yamaguchi et al.(2014)を修正)
解析によって算出された各ケースでの137Csの海への一年間の流出量を図2-2に示す。流出量は各ケースで異なるが、特に陸域での臨界せん断応力が大きい場合(TAU_C-1)、顕著に流出率が低下することが示された。臨界せん断応力は、砂の場合Du Boys式による最大流下容量、シルト・粘土の場合Pathemoneades-Krone 式による侵食・堆積フラックスに影響を与えるが、ここでは特にシルト・粘土の侵食フラックスの低下の影響が大きい結果であった。その次に感度の高いパラメータは放射性セシウムの緩衝深度であった(CS_PROF、αは緩衝深度の逆数)。これらの結果は、より精度の高い解析を行うために、臨界せん断応力や放射性セシウムの深度分布を実測に基づき設定することが重要であることを示している。
図2-3に、前述の基本ケースNORMALにおける100年後までの137Cs沈着量の変遷予測を示す。物理減衰による寄与が大きいものの、土壌の侵食、輸送に伴う放射性セシウムインベントリの低下(いわゆるウェザリング効果)が期待されることが示された。
2.4 今後の課題
ただ、近年測定データが蓄積されたことを受け、上記の解析に対して実測の河川水中137Cs濃度の経時変化と比較すると、実測により得られた濃度低下が解析による予測よりも速いことがわかってきた。現在、深度プロファイルの経時変化や収脱着カイネティクスを考慮することで予測精度の向上を目指した開発を進めている(Liu et al., 2018)。
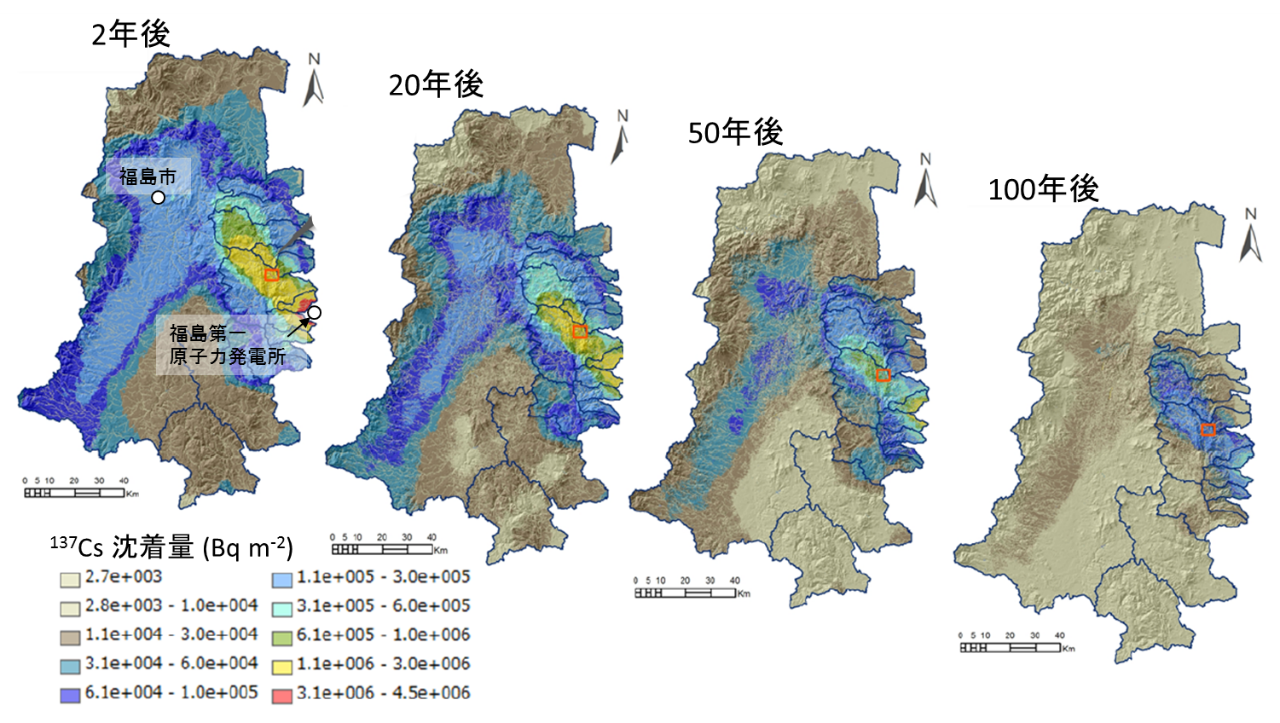
図2-3 基本ケースにおける100年後までの137Cs沈着量の予測マップ(山口ほか(2013)を修正)
3. 流域スケール陸域動態モデル (水循環-土砂-Csの動的モデル)
3.1 目的
流域スケール陸域動態モデルのうち降雨に対する河川流量、土砂、放射性セシウム流出など応答を扱うGETFLOWSを利用した解析的研究の目的は、主に河川から海に流出する放射性セシウムの発生源の解明、生物利用性の高い溶存態放射性セシウムの挙動の評価である。
3.2 手法
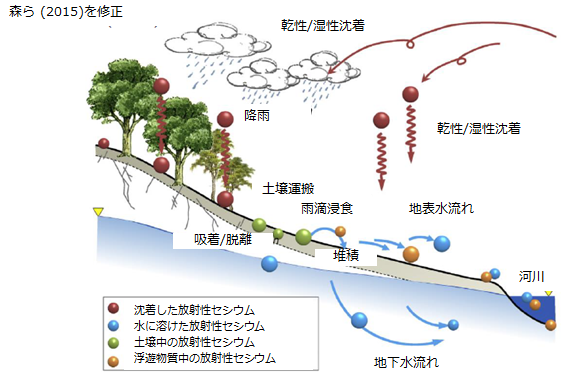
図3-1 GETFLOWS概要(Kitamura et al., 2016より引用)
本研究では、国内で20数年にわたり開発・適用されてきた既存の流域水循環シミュレータGETFLOWS(GEneral purpose Terrestrial fluid-FLOW Simulator)(図3-1)をベースとして、土砂・放射性セシウム輸送解析を実施してきた。
モデルや解析条件、結果の詳細はKitamura et al. (2016)およびSakuma et al. (2017; 2018a: 2018b)に譲り、本報告書は、概要について記載する。以下に各現象の支配方程式を示す。水・空気2相流体に対する支配方程式は以下の通りである。
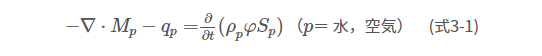
ここで、\( M_p \): 質量フラックス (kg m-2 s-1), \(q_p \):シンク・ソース項 (kg m-3 s-1), \( ρ_p \): 密度 (kg m-3), \( φ \): 有効間隙率 (m3 m-3), \( S_p \): 飽和率 (m3 m-3), \( t \): 時間 (s)である。
地表における土砂輸送に関する支配方程式は以下の通りである。
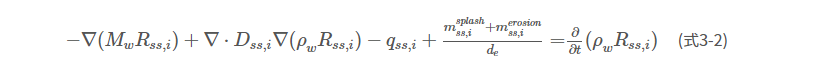
ここで、\( M_w \): 水の質量フラックス (kg m-2 s-1), \( R_{ss,i} \): 粒径成分\( i \)の浮遊砂濃度(kg kg-1), \( D_{ss,i} \): 粒径成分\( i \)の浮遊砂の地表水中の拡散係数 (m2 s-1), \( m^{splash}_{ss,i} \): 粒径成分\( i \)の浮遊砂の雨滴侵食量(kg m-2 s-1), \( m^{erosion}_{ss,i} \) : 地表流による粒径成分\( i \)の浮遊砂の雨滴侵食量(kg m-2 s-1),\( d_{e} \):水深(m),\( q_{ss,i} \):粒形成分\( i \)の浮遊砂のシンク・ソース項(kg m-3 s-1)である。
地表における懸濁態セシウムの輸送および地表地下における溶存態セシウムの輸送に関する支配方程式は以下の通りである。
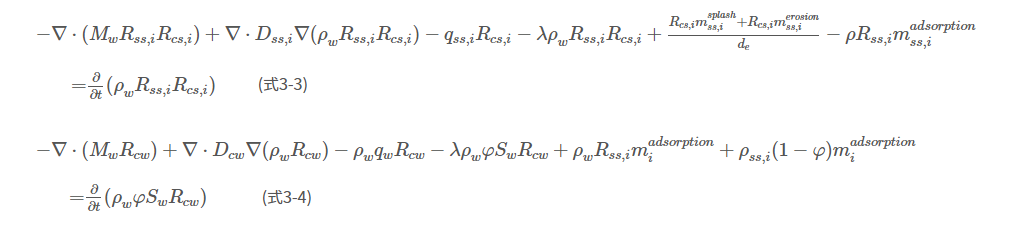
ここで、\( R_{cs,i} \): 粒径成分\( i \)の浮遊砂中の放射性セシウム濃度(Bq kg-1), \( R_{cw} \): 水相中の溶存態セシウム濃度(Bq kg-1), \( D_{cw} \): 流体力学的分散係数(m2 s-1), \( λ \): 崩壊定数 (s-1), \( m^{adsorption}_{ss,i} \): 放射性セシウムと粒径成分\( i \)との収着・脱離量 (Bq kg-1 s-1)である。ただし、(式3-4)の溶存態セシウムに関しては、地表においては左辺の第5項、地下においては左辺の第6項を適用する。
GETFLOWSでは地下流体(水と空気)の一般化ダルシー則と地表流のマニング則を同型式で記述し、地表・地下水の同時計算を可能としている。土砂に関しては、雨滴侵食と地表流による侵食、堆積を考慮し、浮遊砂を複数の粒径土砂(6区分)を解く。表層土壌(土砂交換層)は侵食、堆積の結果を保存し、流域内の侵食・堆積高を計算する。放射性セシウムに関しては、水相中の溶存態、浮遊砂等に収着した懸濁態、土壌・岩石に収着、固定された放射性セシウムについて、放射崩壊と収着分配係数\( K_{d} \)を用いた収脱着方程式を解く。モデルパラメータは観測値を基に水、土砂、放射性セシウムについてキャリブレーション、バリデーションを実施し、再現性のあるモデルを作成し、以下の種々の評価を実施した。
3.3 結果および考察
流域内の放射性セシウム流出解析を実施するに当たり、検討課題としては以下の4つが考えられる。
- 流域間のどういった特徴が流域から流出する放射性セシウム挙動を説明し得るのか
- 濁度や放射性セシウム濃度は出水の規模に応じてどのような応答を示すのか
- 小流域スケールにおいて、どこからどれくらい放射性セシウムが流出してくるのか
- 一般的に用いられている瞬時の収脱着平衡を仮定した\( K_{d} \)モデルを用いて懸濁態セシウムのみならず溶存態セシウム濃度は再現し得るのか
上記4つの問いに対応するために、①福島第一原発近傍の5河川流域(小高川、請戸川、前田川、熊川、富岡川)、②福島県川内村荻ノ沢流域、③福島県太田川上流域を対象に解析を実施した(図3-2)。GETFLOWSを用いて計算を実施するために、種々のデータを集約して、3次元水理地質構造モデルを作成する必要がある。図3-3~3-5に地質構造モデルを示す。地質構造モデルの各層に対して絶対浸透率などの地下水流れに係るパラメータを与え、また土地利用や地表土壌分布に基づいて蒸発散や表層流れに係るパラメータを設定することで、水理地質構造モデルを構築した。
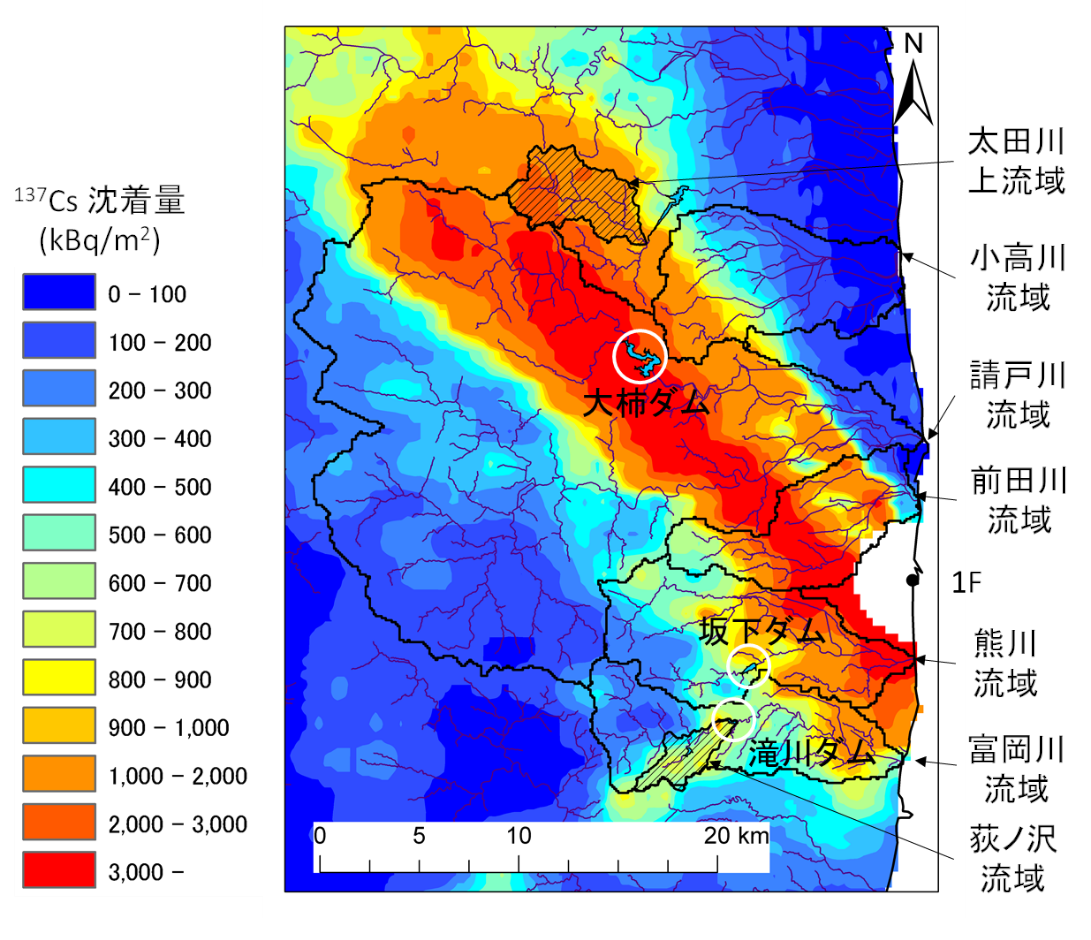
図3-2 1F 近傍の5 河川流域(小高川、請戸川、前田川、熊川、富岡川)および太田川上流域、富岡川流域内の荻ノ沢流域における137Cs 沈着量の分布(第4次航空機モニタリングデータ、2011年11月)
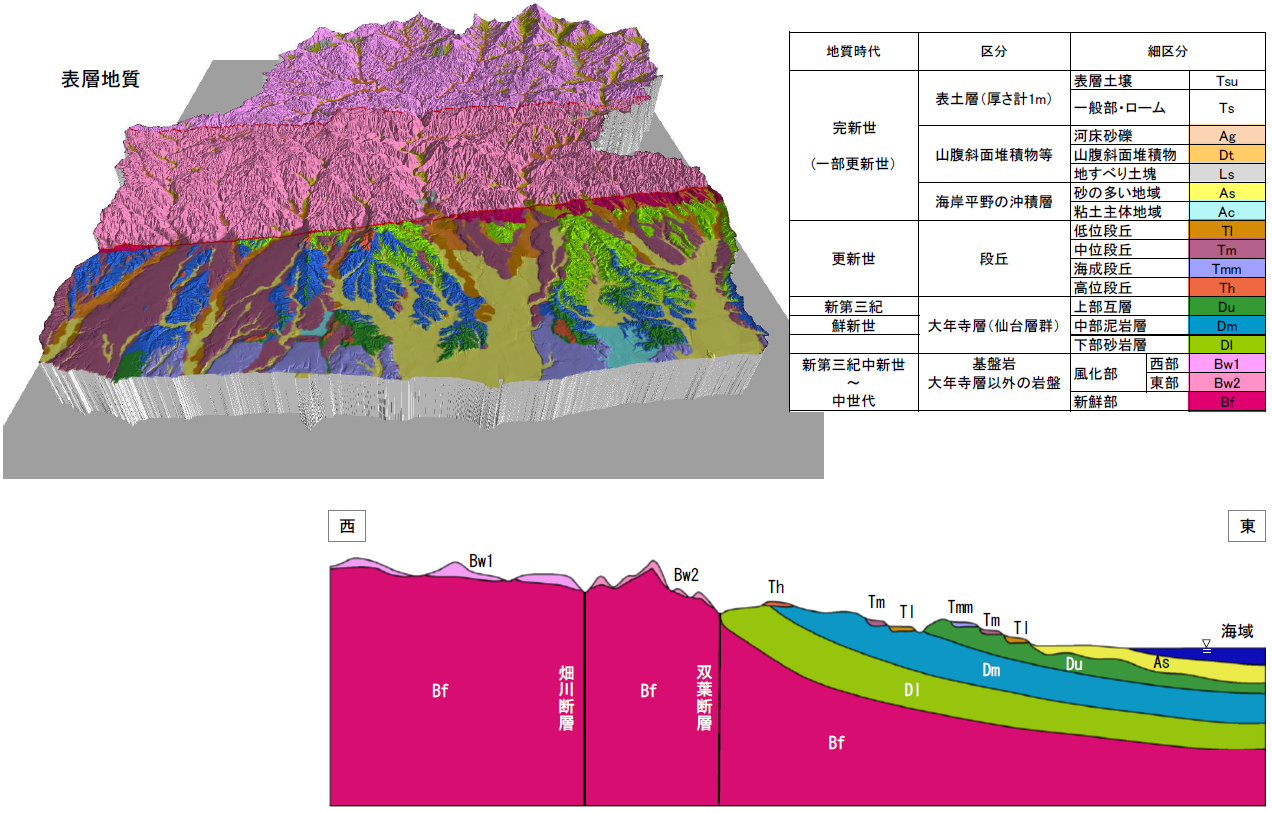
図3-3 3次元地質構造モデル(小高川、請戸川、前田川、熊川、富岡川流域)
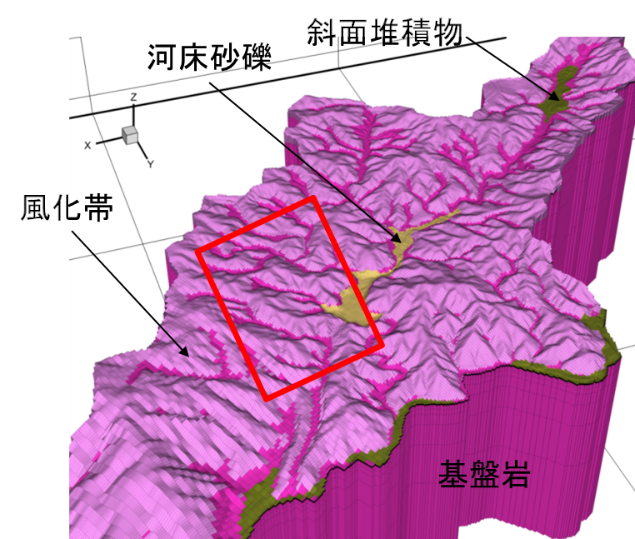
図3-4 3次元地質構造モデル(荻ノ沢流域)
赤枠は図3-9の領域を示す。
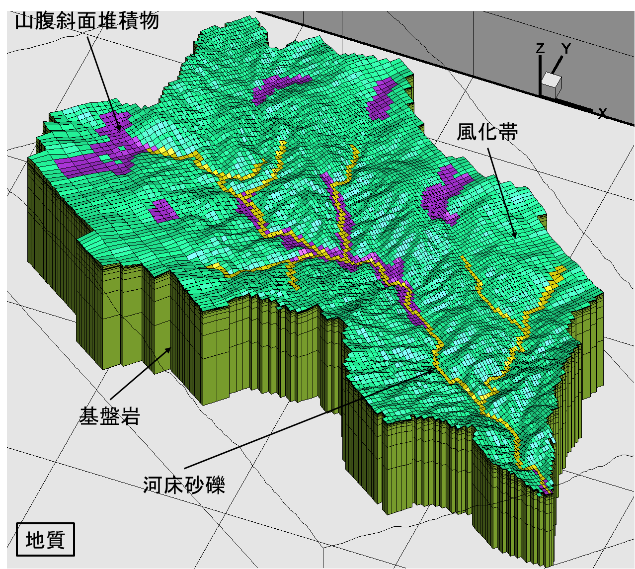
図3-5 3次元地質構造モデル(太田川上流域)
①について、5河川流域を対象に、異なる降雨強度の雨の流出シミュレーションを実施し、流域のどのような特徴が流域からの放射性セシウム流出に寄与しているのかを評価した。対象とする流域の特徴は、表3-1に示す。対象とする降雨イベントは、2011年9月の台風15号(Roke)、2013年9月の台風18号(Man-yi)および10月の26号(Wipha)である。
表3-1 各流域の特徴
| (単位) | 流域面積 | 森林 | 水田 | その他 | 初期沈着量(137Cs) |
|---|---|---|---|---|---|
| km2 | % | % | % | TBq | |
| 小高川 | 68 | 49 | 26 | 25 | 48 |
| 請戸川 | 68 | 57 | 25 | 18 | 833 |
| 前田川 | 45 | 75 | 8 | 17 | 72 |
| 熊川 | 75 | 71 | 14 | 15 | 86 |
| 富岡川 | 62 | 71 | 13 | 16 | 38 |
| 荻ノ沢(富岡川水系) | 7.7 | 92 | 2 | 6 | 5.5 |
| 太田川上流 | 21 | 99 | 0 | 1 | 40 |
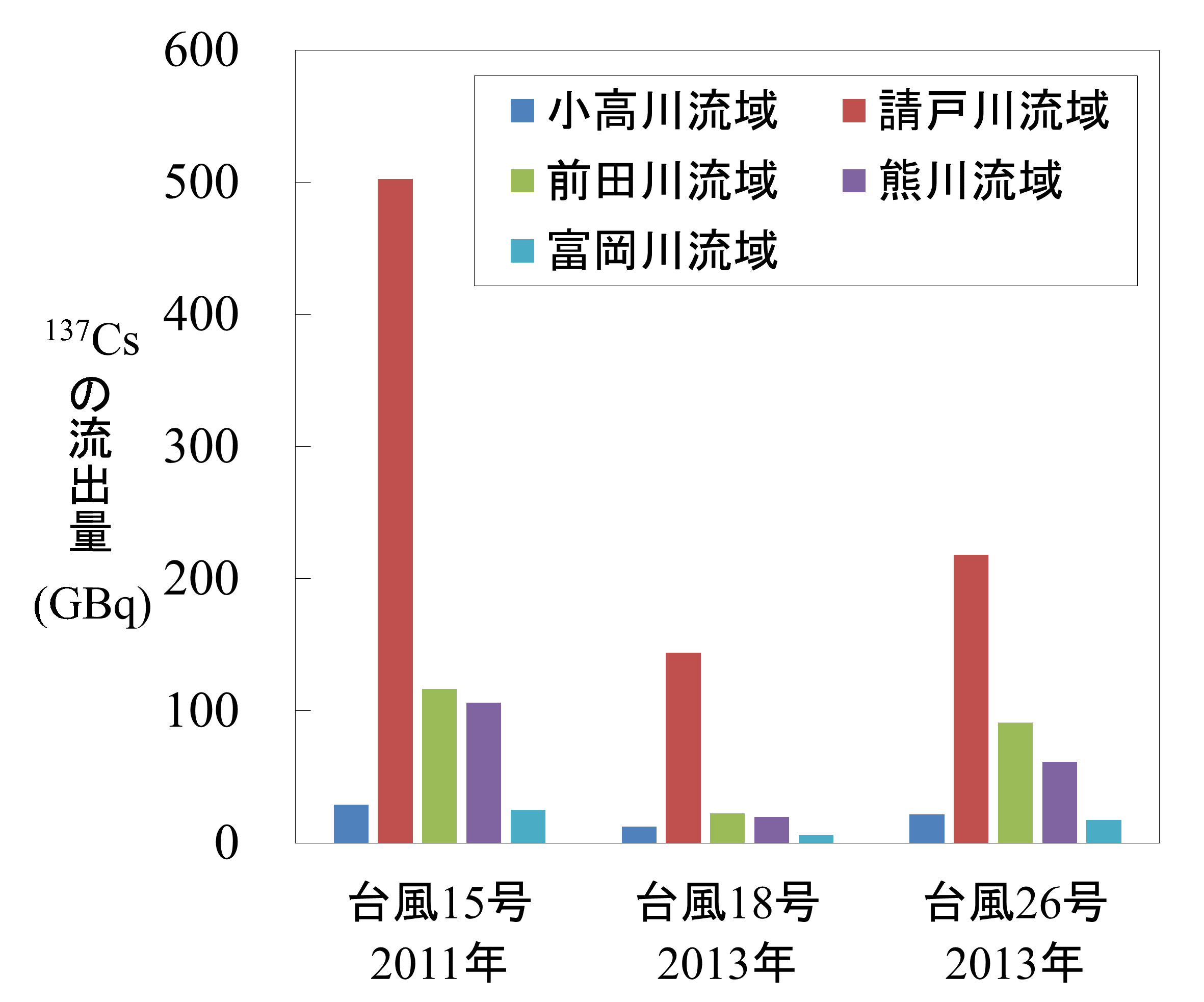
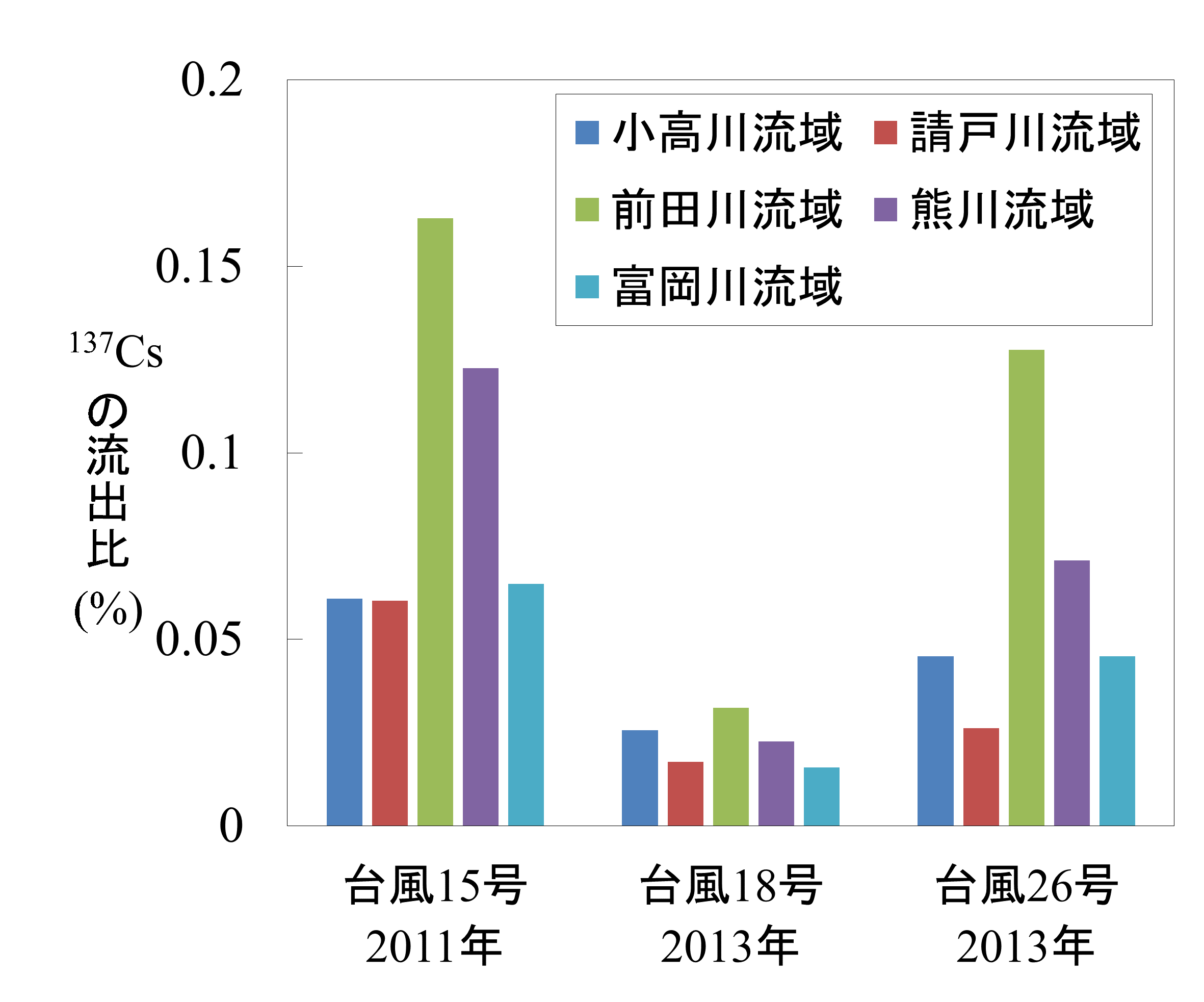
図3-6 台風等の豪雨時における5 河川流域からの137Cs の(a)流出量と(b)流出比
図3-6の左図に示す通り、流出量(GBq)は流域面積が大きく、沈着量が大きい請戸川流域(表3-1)が最大となった(約144-503 GBq)。次いで前田川流域(約23-117 GBq)、熊川(20-106 GBq)、小高川(約12-29 GBq)、富岡川(約6-25 GBq)である。しかし、流出量を流域の沈着量で除した流出比を用いて評価すると、むしろ請戸川は最小となり(約0.02-0.06%)、前田川が最大(約0.03-0.16%)となった。上流からの土砂をせき止める効果のあるダムの存在は、懸濁態セシウムの下流への流出を抑制し、さらに、森林は地表で水流が発生しにくいため、土砂の流出量が少なくなる。これらのことから、森林が大部分を占めるダム湖の上流域に多くの放射性セシウムが存在する請戸川流域では、流出が抑制され、結果として流出比が小さくなったと考えられ、一方、前田川流域では、ダムが存在せず、土砂の流出量が多い水田の分布域で沈着量が多いため、流出比が大きくなったことがわかった。すなわち、放射性セシウムの河川から海への流出率は、ダムがある河川流域では低く、流域内で沈着量の多い土地が水田などの場合に高い傾向があることがわかった(Sakuma et al., 2017)。
続いて、ダム放流工や頭首工での取水管理の判断材料を提供する観点から、降雨強度と濁度、放射性セシウム濃度の関係を評価するために、様々な降雨パターン(図3-7)に対するダム放流工や頭首工での濁度や放射性セシウム濃度の応答を解析で推定した。図3-8に結果の一例を示す。
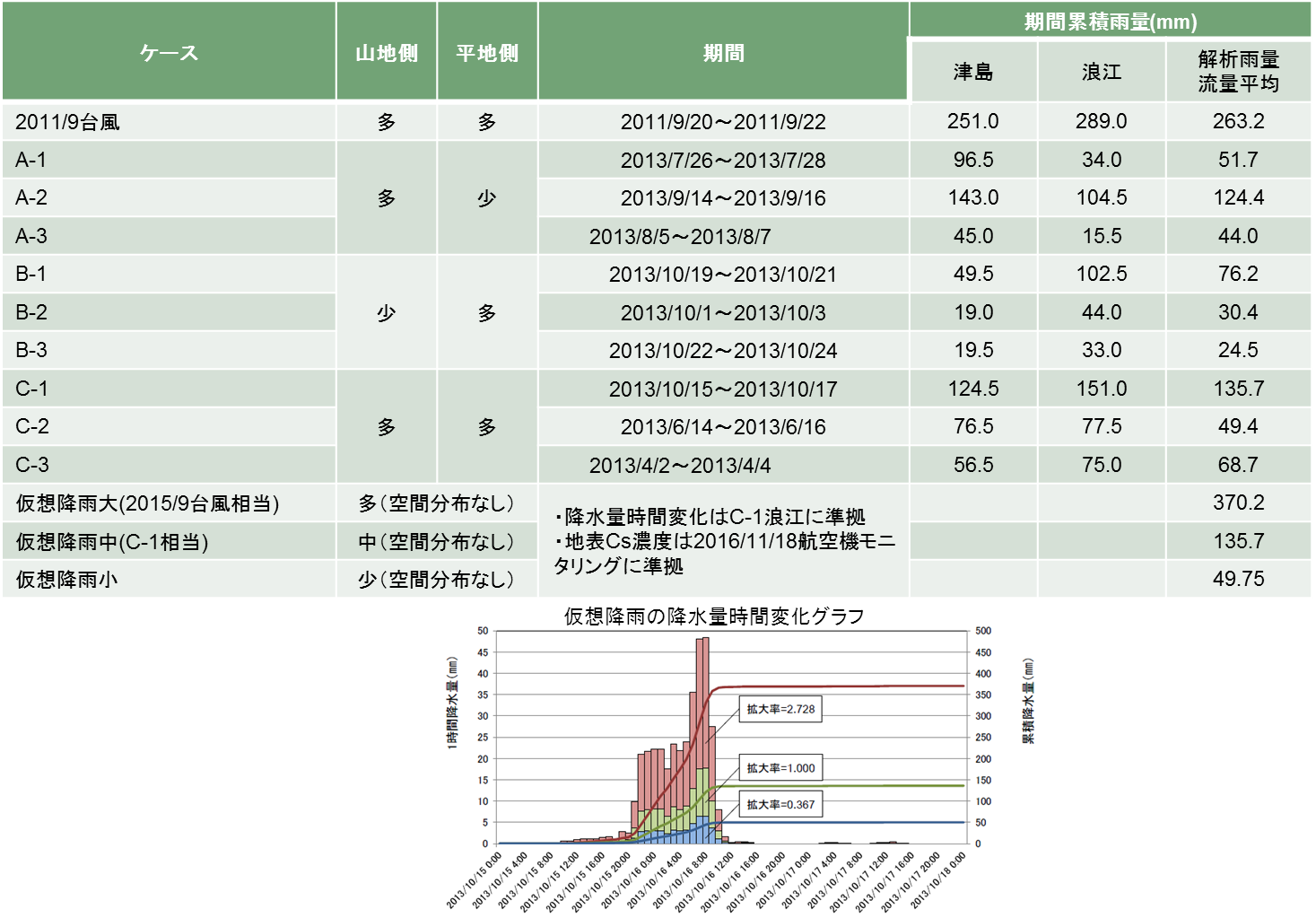
図3-7 適用した降雨パターン
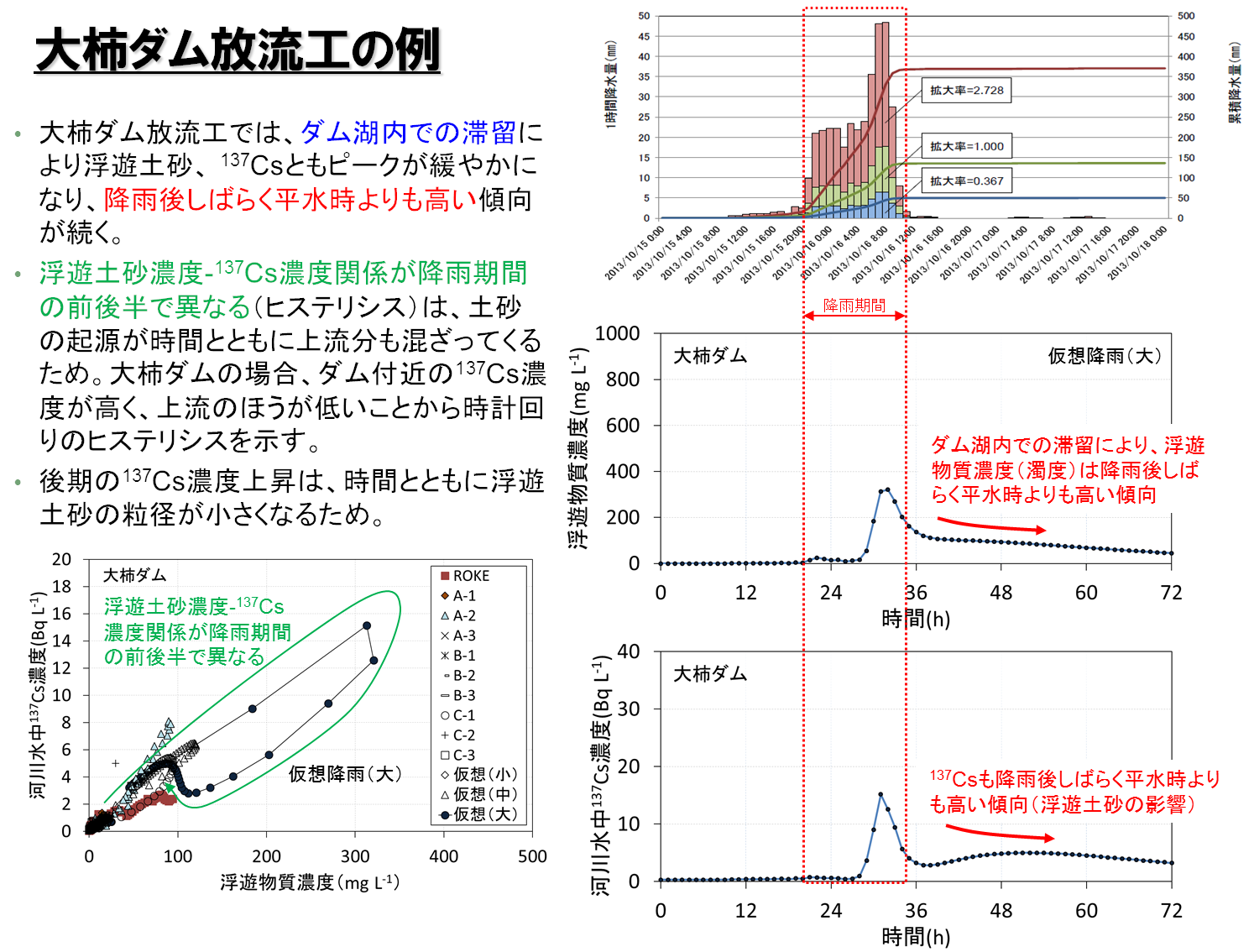
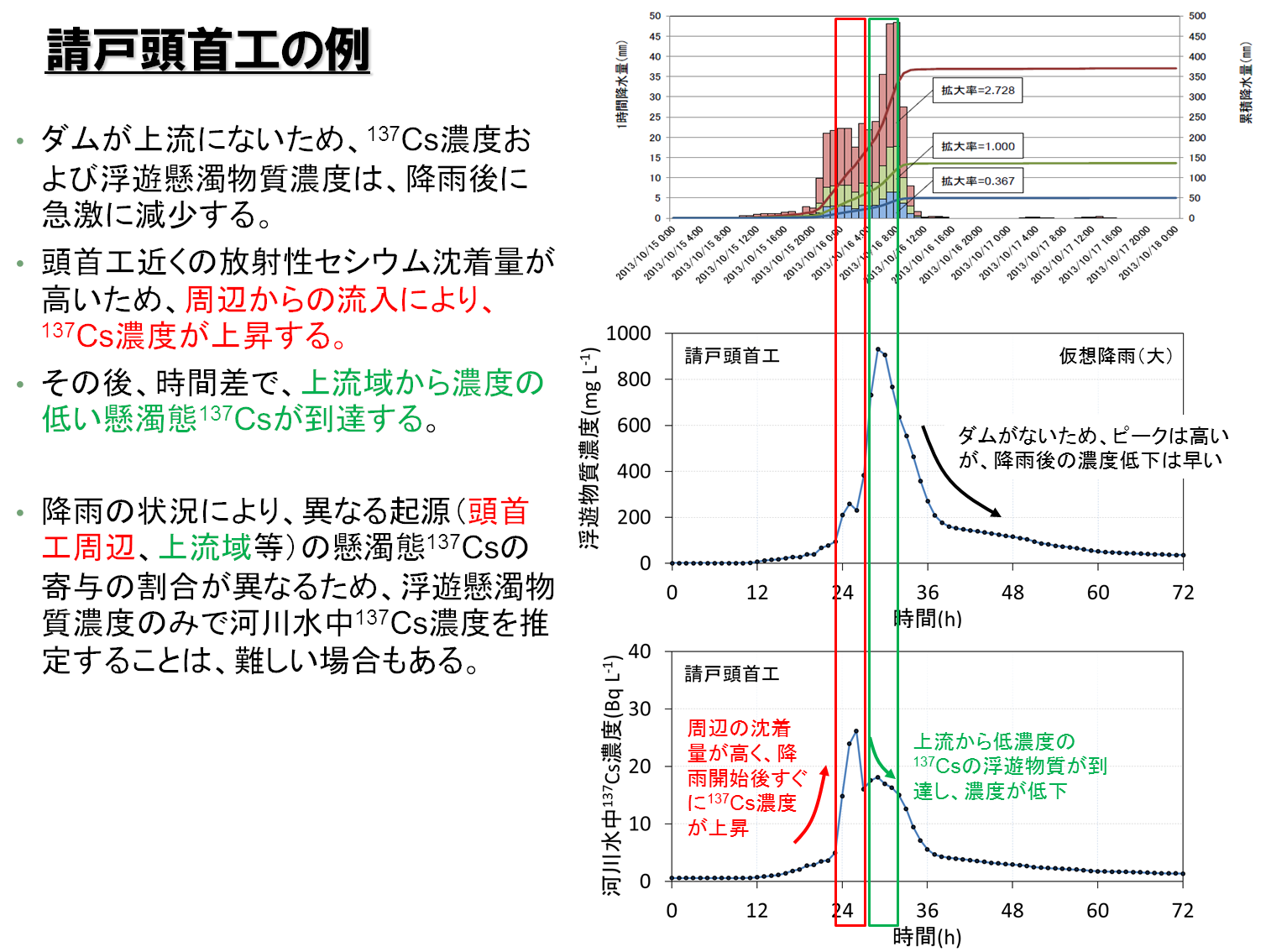
図3-8 解析結果の例
請戸川上流域に位置する大柿ダム放流工においては、ダム湖内での滞留により、浮遊土砂濃度、放射性セシウムともピークが緩やかになり、降雨後しばらく平水時に比べ高い傾向が続いた。浮遊土砂濃度-放射性セシウム濃度関係が降雨期間の前後半で異なる(ヒステリシス)のは、土砂の起源が時間の経過とともに上流分が到達するためと考えられる。大柿ダムの場合は、ダム付近の沈着量が高く、上流域の方が相対的に低いことから、時間の経過ともに濃度が減少し、時計回りのヒステリシスを示すと考えられた。請戸川の支流である高瀬川に位置する請戸頭首工においても、同様のヒステリシスの影響によって浮遊土砂濃度と放射性セシウム濃度が1対1に対応せず、浮遊土砂濃度のみで河川水中の放射性セシウム濃度を推定することは難しい場合もあることが示唆された。さらに、本解析では2013年の一部の河川のデータに基づいてモデルを検証している(Kitamura et al., 2016およびSakuma et al., 2017)が、経時変化する河川中の放射性セシウム濃度の検証は十分でないことにも留意する必要がある。
②について、福島県川内村荻ノ沢流域を対象に、前述と比較し、非常に詳細な格子(約10 m)を用いて、平水時および出水時を含む、事故後約4年半(2011年5月26日~2015年12月31日)の流出解析を実施することで、流域内のどこからどれくらい土砂と放射性セシウムが流出しているのかを評価した。流域特徴は表3-1に示す。
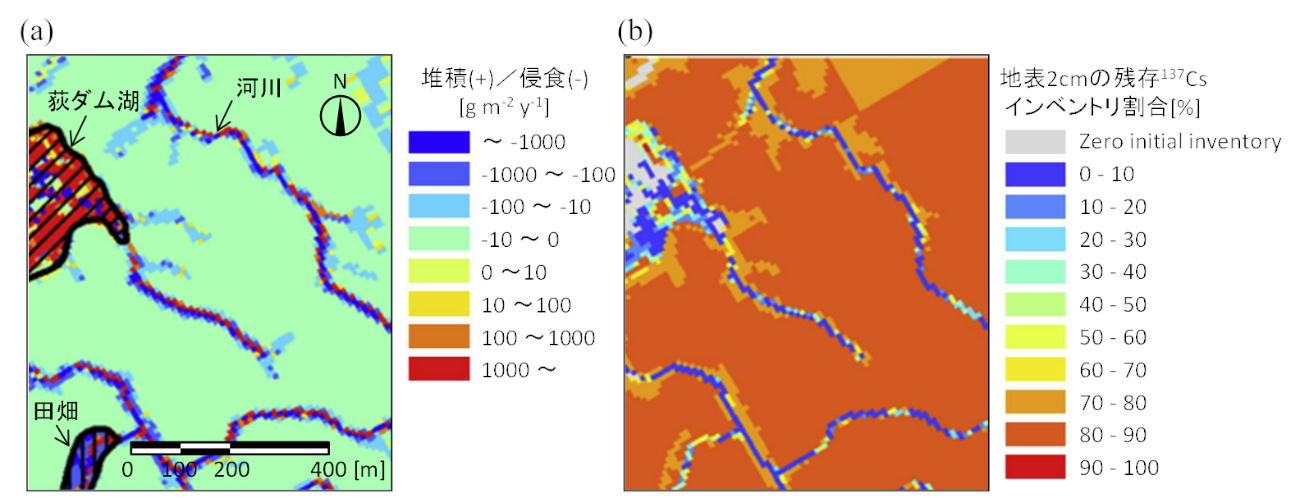
図3-9 2011年5月から2015年12月までの期間における(a)侵食・堆積量および(b)残存137Cs割合
図3-9に示す通り、河川近傍や森林の沢沿いでの侵食量および放射性セシウムのインベントリ低下割合が大きく、河川から離れた森林での侵食はほとんど生じておらず(総侵食量:0.001-0.1 mm)、放射性セシウムインベントリの低下率は小さかった。定量的には、河川近傍からの寄与は、河川から離れた森林からの寄与に比べ1桁ほど大きいことがわかった(Sakuma et al., 2018a)。
③について、南相馬市・浪江町太田川上流域を対象に、森林流域から流出する溶存態セシウム濃度は、水、土砂、懸濁態セシウム流出を再現した精緻なモデルを用いて表現可能かどうかを評価した。流域の特徴は表3-1に示す。また設定した分配係数\( K_{d} \)の値を表3-2に示す。
表3-2 設定した分配係数\( K_{d} \)
| 代表粒径 | Case 1 | Case 2 |
|---|---|---|
| µm | \( K_d \) (m3 kg-1) | \( K_d \) (m3 kg-1) |
| 1 | 200 | 200 |
| 10 | 200 | 200 |
| 100 | 200 | 50 |
| 300 | 200 | 50 |
| 1000 | 0 | 0 |
| 5000 | 0 | 0 |
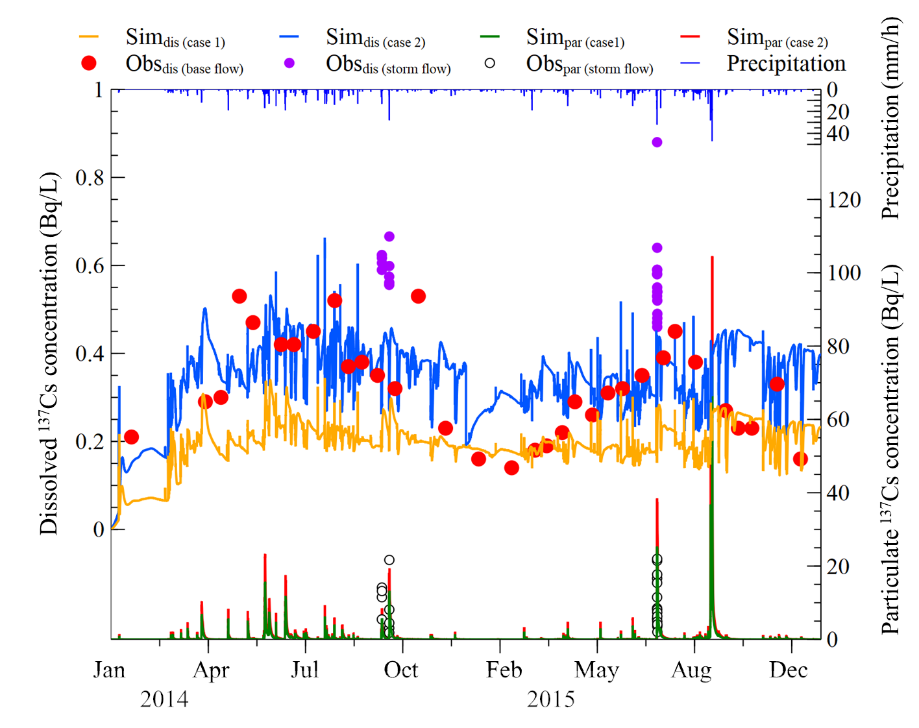
図3-10 懸濁態・溶存態セシウムの観測値と計算値の比較
図3-10のグラフから河川水中の平水時の溶存態セシウム濃度の観測値は0.14-0.53 Bq L-1(平均0.32 Bq L-1)であったが、セシウムへの収着特性の粒径による違いを考慮することによって、ある程度説明できることがわかった(図3-10の溶存態Cs(ケース2)(平均0.36 Bq L-1))。しかし、実測で観測されている溶存態セシウム濃度の季節変動(夏季に高く、冬季に低い)や降雨時の変動(0.18-0.88 Bq L-1, 平均0.55 Bq L-1)について、現状の\( K_d \)モデルのみでは表現することが難しいことがわかった。これは、落葉層の微生物分解等が関与していることを示唆している(Sakuma et al., 2018b)。
3.4 今後の課題
森林流域から流出する溶存態セシウム濃度を再現するために、森林生態系コンパートメントモデルをGETFLOWSにカップリングすることによって、季節変動や出水時の濃度上昇を表現可能なモデルを開発する予定である。さらに溶存態セシウムの発生源や発生経路、有機物からの溶存態セシウム溶脱パラメータ等を取得し、モデルへフィードバックしつつメカニズムの解明を目指す。